discrete uniformProbability mass function 
n = 5 where n = b − a + 1 |
Cumulative distribution function 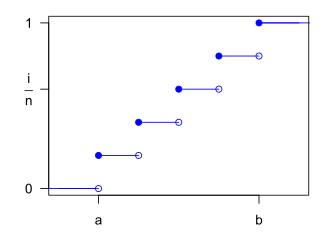
|
| Notation |  or or  |
|---|
| Parameters | 

 |
|---|
| Support |  |
|---|
| pmf |  |
|---|
| CDF |  |
|---|
| Mean |  |
|---|
| Median |  |
|---|
| Mode | N/A |
|---|
| Variance |  |
|---|
| Skewness |  |
|---|
| Ex. kurtosis |  |
|---|
| Entropy |  |
|---|
| MGF |  |
|---|
| CF |  |
|---|
In probability theory and statistics, the discrete uniform distribution is a symmetric probability distribution whereby a finite number of values are equally likely to be observed; every one of n values has equal probability 1/n. Another way of saying "discrete uniform distribution" would be "a known, finite number of outcomes equally likely to happen".
A simple example of the discrete uniform distribution is throwing a fair dice. The possible values are 1, 2, 3, 4, 5, 6, and each time the dice is thrown the probability of a given score is 1/6. If two dice are thrown and their values added, the resulting distribution is no longer uniform since not all sums have equal probability.
The discrete uniform distribution itself is inherently non-parametric. It is convenient, however, to represent its values generally by all integers in an interval [a,b], so that a and b become the main parameters of the distribution (often one simply considers the interval [1,n] with the single parameter n). With these conventions, the cumulative distribution function (CDF) of the discrete uniform distribution can be expressed, for any k ∈ [a,b], as

Estimation of maximum[edit]
This example is described by saying that a sample of k observations is obtained from a uniform distribution on the integers  , with the problem being to estimate the unknown maximum N. This problem is commonly known as the German tank problem, following the application of maximum estimation to estimates of German tank production during World War II.
, with the problem being to estimate the unknown maximum N. This problem is commonly known as the German tank problem, following the application of maximum estimation to estimates of German tank production during World War II.
The uniformly minimum variance unbiased (UMVU) estimator for the maximum is given by

where m is the sample maximum and k is the sample size, sampling without replacement.[1] This can be seen as a very simple case of maximum spacing estimation.
This has a variance of[1]

so a standard deviation of approximately  , the (population) average size of a gap between samples; compare
, the (population) average size of a gap between samples; compare  above.
above.
The sample maximum is the maximum likelihood estimator for the population maximum, but, as discussed above, it is biased.
If samples are not numbered but are recognizable or markable, one can instead estimate population size via the capture-recapture method.
Derivation[edit]
For any integer m such that k ≤ m ≤ N, the probability that the sample maximum will be equal to m can be computed as follows. The number of different groups of k tanks that can be made from a total of N tanks is given by the binomial coefficient  . Since in this way of counting the permutations of tanks are counted only once, we can order the serial numbers and take note of the maximum of each sample. To compute the probability we have to count the number of ordered samples that can be formed with the last element equal to m and all the other k-1 tanks less or equal to m-1. The number of samples of k-1 tanks that can be made from a total m-1 tanks is given by the binomial coefficient
. Since in this way of counting the permutations of tanks are counted only once, we can order the serial numbers and take note of the maximum of each sample. To compute the probability we have to count the number of ordered samples that can be formed with the last element equal to m and all the other k-1 tanks less or equal to m-1. The number of samples of k-1 tanks that can be made from a total m-1 tanks is given by the binomial coefficient  , so the probability of having a maximum m is
, so the probability of having a maximum m is  .
.
Given the total number N and the sample size k, the expected value of the sample maximum is
![{\displaystyle {\begin{aligned}\mu =\mathrm {E} [m]&=\sum _{m=k}^{N}m{\frac {\tbinom {m-1}{k-1}}{\tbinom {N}{k}}}\\&={\frac {1}{(k-1)!{\tbinom {N}{k}}}}\sum _{m=k}^{N}{\frac {m!}{(m-k)!}}\\&={\frac {k!}{(k-1)!{\tbinom {N}{k}}}}\sum _{m=k}^{N}{\tbinom {m}{k}}\\&=k{\frac {\tbinom {N+1}{k+1}}{\tbinom {N}{k}}}\\&={\frac {k(N+1)}{k+1}},\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/23170ba302df742e8614d7cf4399c48636828c06)
where the hockey-stick identity  was used.
was used.
From this equation, the unknown quantity N can be expressed in terms of expectation and sample size as

By linearity of the expectation, it is obtained that
![{\displaystyle {\begin{aligned}\mu \left(1+k^{-1}\right)-1&=\mathrm {E} \left[m\left(1+k^{-1}\right)-1\right],\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f6726c1a12f893fd011a31b3f4ef85ed8fde67da)
and so an unbiased estimator of N is obtained by replacing the expectation with the observation,

Besides being unbiased this estimator also attains minimum variance. To show this, first note that the sample maximum is a sufficient statistic for the population maximum since the probability P(m;N) is expressed as a function of m alone. Next it must be shown that the statistics m is also a complete statistic, a special kind of sufficient statistics (demonstration pending). Then the Lehmann–Scheffé theorem implies that  is the minimum-variance unbiased estimator of N.[2]
is the minimum-variance unbiased estimator of N.[2]
The variance of the estimator is calculated from the variance of the sample maximum
![{\displaystyle {\begin{aligned}\mathrm {Var} [{\hat {N}}]&={\frac {(k+1)^{2}}{k^{2}}}\mathrm {Var} [m].\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4d8fa69e9a1c6a8afb1ed7eed054d6711657a8ea)
The variance of the maximum is in turn calculated from the expected values of  and
and  . The calculation of the expected value of
. The calculation of the expected value of  is,
is,
![{\displaystyle {\begin{aligned}\mathrm {E} [m^{2}]&=\sum _{m=k}^{N}m^{2}{\frac {\tbinom {m-1}{k-1}}{\tbinom {N}{k}}}\\&={\frac {1}{(k-1)!{\tbinom {N}{k}}}}\sum _{m=k}^{N}m{\frac {m!}{(m-k)!}}\\&={\frac {1}{(k-1)!{\tbinom {N}{k}}}}\sum _{m=k}^{N}(m+1-1){\frac {m!}{(m-k)!}}\\&={\frac {1}{(k-1)!{\tbinom {N}{k}}}}\sum _{m=k}^{N}{\frac {(m+1)!}{(m-k)!}}-{\frac {1}{(k-1)!{\tbinom {N}{k}}}}\sum _{m=k}^{N}{\frac {m!}{(m-k)!}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/badb7b87eae8e7ab0aba1a5e655e967caaab25bf)
where the second term is the expected value of  . The first term can be expressed in terms of k and N,
. The first term can be expressed in terms of k and N,

where the replacement  was made and the hockey-stick identity used. Replacing this result and the expectation of
was made and the hockey-stick identity used. Replacing this result and the expectation of  in the equation of
in the equation of ![{\displaystyle E[m^{2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/04b8b1fb5c2054708e5f835ab5ae0d0ffe985ff5) ,
,
![{\displaystyle {\begin{aligned}\mathrm {E} [m^{2}]&={\frac {k(N+2)(N+1)}{(k+2)}}-{\frac {k(N+1)}{k+1}}\\&=k(N+1){\Big (}{\frac {N+2}{k+2}}-{\frac {1}{k+1}}{\Big )}\\&={\frac {k(N+1)(kN+k+N)}{(k+1)(k+2)}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/236f18aacd1f9000a132377bfc24ab34a6ee9c5b)
The variance of  is then obtained,
is then obtained,
![{\displaystyle {\begin{aligned}\mathrm {Var} [m]&=\mathrm {E} [m^{2}]-\mathrm {E} [m]^{2}\\&={\frac {k(N+1)}{(k+1)}}{\Big (}{\frac {kN+k+N}{k+2}}-{\frac {k(N+1)}{k+1}}{\Big )}\\&={\frac {k(N+1)}{(k+1)}}{\frac {(N-k)}{(k+2)(k+1)}}\\&={\frac {k(N+1)(N-k)}{(k+1)^{2}(k+2)}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c6db7102699fb7a2357727ad9b1cdb44f3c4d2a8)
Finally the variance of the estimator  can be calculated,
can be calculated,
![{\displaystyle {\begin{aligned}\mathrm {Var} [{\hat {N}}]&={\frac {(k+1)^{2}}{k^{2}}}\mathrm {Var} [m]\\&={\frac {(k+1)^{2}}{k^{2}}}{\frac {k(N+1)(N-k)}{(k+1)^{2}(k+2)}}\\&={\frac {(N+1)(N-k)}{k(k+2)}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d27de49b7ad0676141e8d5d2300850e434053419)
Random permutation[edit]
See rencontres numbers for an account of the probability distribution of the number of fixed points of a uniformly distributed random permutation.
See also[edit]
References[edit]
|
|---|
|
Discrete univariate
with finite support | |
|---|
Discrete univariate
with infinite support | |
|---|
Continuous univariate
supported on a bounded interval | |
|---|
Continuous univariate
supported on a semi-infinite interval | |
|---|
Continuous univariate
supported on the whole real line | |
|---|
Continuous univariate
with support whose type varies | |
|---|
| Mixed continuous-discrete univariate | |
|---|
| Multivariate (joint) | |
|---|
| Directional | |
|---|
| Degenerate and singular | |
|---|
| Families | |
|---|


























![{\displaystyle {\begin{aligned}\mu =\mathrm {E} [m]&=\sum _{m=k}^{N}m{\frac {\tbinom {m-1}{k-1}}{\tbinom {N}{k}}}\\&={\frac {1}{(k-1)!{\tbinom {N}{k}}}}\sum _{m=k}^{N}{\frac {m!}{(m-k)!}}\\&={\frac {k!}{(k-1)!{\tbinom {N}{k}}}}\sum _{m=k}^{N}{\tbinom {m}{k}}\\&=k{\frac {\tbinom {N+1}{k+1}}{\tbinom {N}{k}}}\\&={\frac {k(N+1)}{k+1}},\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/23170ba302df742e8614d7cf4399c48636828c06)


![{\displaystyle {\begin{aligned}\mu \left(1+k^{-1}\right)-1&=\mathrm {E} \left[m\left(1+k^{-1}\right)-1\right],\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f6726c1a12f893fd011a31b3f4ef85ed8fde67da)


![{\displaystyle {\begin{aligned}\mathrm {Var} [{\hat {N}}]&={\frac {(k+1)^{2}}{k^{2}}}\mathrm {Var} [m].\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4d8fa69e9a1c6a8afb1ed7eed054d6711657a8ea)


![{\displaystyle {\begin{aligned}\mathrm {E} [m^{2}]&=\sum _{m=k}^{N}m^{2}{\frac {\tbinom {m-1}{k-1}}{\tbinom {N}{k}}}\\&={\frac {1}{(k-1)!{\tbinom {N}{k}}}}\sum _{m=k}^{N}m{\frac {m!}{(m-k)!}}\\&={\frac {1}{(k-1)!{\tbinom {N}{k}}}}\sum _{m=k}^{N}(m+1-1){\frac {m!}{(m-k)!}}\\&={\frac {1}{(k-1)!{\tbinom {N}{k}}}}\sum _{m=k}^{N}{\frac {(m+1)!}{(m-k)!}}-{\frac {1}{(k-1)!{\tbinom {N}{k}}}}\sum _{m=k}^{N}{\frac {m!}{(m-k)!}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/badb7b87eae8e7ab0aba1a5e655e967caaab25bf)


![{\displaystyle E[m^{2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/04b8b1fb5c2054708e5f835ab5ae0d0ffe985ff5)
![{\displaystyle {\begin{aligned}\mathrm {E} [m^{2}]&={\frac {k(N+2)(N+1)}{(k+2)}}-{\frac {k(N+1)}{k+1}}\\&=k(N+1){\Big (}{\frac {N+2}{k+2}}-{\frac {1}{k+1}}{\Big )}\\&={\frac {k(N+1)(kN+k+N)}{(k+1)(k+2)}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/236f18aacd1f9000a132377bfc24ab34a6ee9c5b)
![{\displaystyle {\begin{aligned}\mathrm {Var} [m]&=\mathrm {E} [m^{2}]-\mathrm {E} [m]^{2}\\&={\frac {k(N+1)}{(k+1)}}{\Big (}{\frac {kN+k+N}{k+2}}-{\frac {k(N+1)}{k+1}}{\Big )}\\&={\frac {k(N+1)}{(k+1)}}{\frac {(N-k)}{(k+2)(k+1)}}\\&={\frac {k(N+1)(N-k)}{(k+1)^{2}(k+2)}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c6db7102699fb7a2357727ad9b1cdb44f3c4d2a8)
![{\displaystyle {\begin{aligned}\mathrm {Var} [{\hat {N}}]&={\frac {(k+1)^{2}}{k^{2}}}\mathrm {Var} [m]\\&={\frac {(k+1)^{2}}{k^{2}}}{\frac {k(N+1)(N-k)}{(k+1)^{2}(k+2)}}\\&={\frac {(N+1)(N-k)}{k(k+2)}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d27de49b7ad0676141e8d5d2300850e434053419)