Training, validation, and test sets

From Wikipedia, the free encyclopedia
  (Redirected from Training set)
Jump to navigation Jump to search

In machine learning, the study and construction of algorithms that can learn from and make predictions on data[1] is a common task. Such algorithms work by making data-driven predictions or decisions,[2]:2 through building a mathematical model from input data.

The data used to build the final model usually comes from multiple datasets. In particular, three data sets are commonly used in different stages of the creation of the model.

The model is initially fit on a training dataset,[3] that is a set of examples used to fit the parameters (e.g. weights of connections between neurons in artificial neural networks) of the model.[4] The model (e.g. a neural net or a naive Bayes classifier) is trained on the training dataset using a supervised learning method (e.g. gradient descent or stochastic gradient descent). In practice, the training dataset often consist of pairs of an input vector (or scalar) and the corresponding output vector (or scalar), which is commonly denoted as the target (or label). The current model is run with the training dataset and produces a result, which is then compared with the target, for each input vector in the training dataset. Based on the result of the comparison and the specific learning algorithm being used, the parameters of the model are adjusted. The model fitting can include both variable selection and parameter estimation.

Successively, the fitted model is used to predict the responses for the observations in a second dataset called the validation dataset.[3] The validation dataset provides an unbiased evaluation of a model fit on the training dataset while tuning the model's hyperparameters [5] (e.g. the number of hidden units in a neural network[4]). Validation datasets can be used for regularization by early stopping: stop training when the error on the validation dataset increases, as this is a sign of overfitting to the training dataset.[6] This simple procedure is complicated in practice by the fact that the validation dataset's error may fluctuate during training, producing multiple local minima. This complication has led to the creation of many ad-hoc rules for deciding when overfitting has truly begun.[6]

Finally, the test dataset is a dataset used to provide an unbiased evaluation of a final model fit on the training dataset.[5] When the data in the test dataset has never been used in training (for example in cross-validation), the test dataset is also called a holdout dataset.

Training dataset[edit]

A training dataset is a dataset of examples used for learning, that is to fit the parameters (e.g., weights) of, for example, a classifier.[7][8]

Most approaches that search through training data for empirical relationships tend to overfit the data, meaning that they can identify and exploit apparent relationships in the training data that do not hold in general.

Validation dataset[edit]

A validation dataset is a dataset of examples used to tune the hyperparameters (i.e. the architecture) of a classifier. It is sometimes also called the development set or the "dev set". In artificial neural networks, a hyperparameter is, for example, the number of hidden units.[7][8] It, as well as the testing set (as mentioned above), should follow the same probability distribution as the training dataset.

In order to avoid overfitting, when any classification parameter needs to be adjusted, it is necessary to have a validation dataset in addition to the training and test datasets. For example, if the most suitable classifier for the problem is sought, the training dataset is used to train the candidate algorithms, the validation dataset is used to compare their performances and decide which one to take and, finally, the test dataset is used to obtain[citation needed] the performance characteristics such as accuracy, sensitivity, specificity, F-measure, and so on. The validation dataset functions as a hybrid: it is training data used by testing, but neither as part of the low-level training nor as part of the final testing[citation needed].

The basic process of using a validation dataset for model selection (as part of training dataset, validation dataset, and test dataset) is:[8][9]

Since our goal is to find the network having the best performance on new data, the simplest approach to the comparison of different networks is to evaluate the error function using data which is independent of that used for training. Various networks are trained by minimization of an appropriate error function defined with respect to a training data set. The performance of the networks is then compared by evaluating the error function using an independent validation set, and the network having the smallest error with respect to the validation set is selected. This approach is called the hold out method. Since this procedure can itself lead to some overfitting to the validation set, the performance of the selected network should be confirmed by measuring its performance on a third independent set of data called a test set.

An application of this process is in early stopping, where the candidate models are successive iterations of the same network, and training stops when the error on the validation set grows, choosing the previous model (the one with minimum error).

Test dataset[edit]

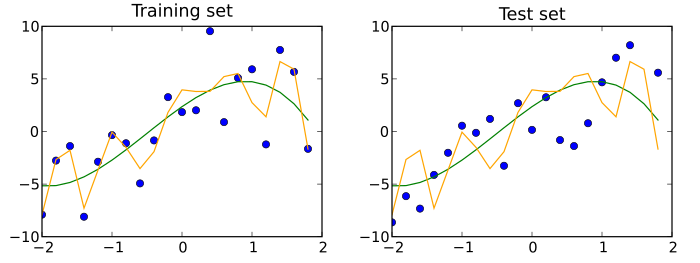
A test dataset is a dataset that is independent of the training dataset, but that follows the same probability distribution as the training dataset. If a model fit to the training dataset also fits the test dataset well, minimal overfitting has taken place (see figure below). A better fitting of the training dataset as opposed to the test dataset usually points to overfitting.

A test set is therefore a set of examples used only to assess the performance (i.e. generalization) of a fully specified classifier.[7][8]

A training set (left) and a test set (right) from the same statistical population are shown as blue points. Two predictive models are fit to the training data. Both fitted models are plotted with both the training and test sets. In the training set, the MSE of the fit shown in orange is 4 whereas the MSE for the fit shown in green is 9. In the test set, the MSE for the fit shown in orange is 15 and the MSE for the fit shown in green is 13. The orange curve severely overfits the training data, since its MSE increases by almost a factor of four when comparing the test set to the training set. The green curve overfits the training data much less, as its MSE increases by less than a factor of 2.

Holdout dataset[edit]

Most simply, part of the original dataset can be set aside and used as a test set: this is known as the holdout method[10].

Cross-validation[edit]

A dataset can be repeatedly split into a training dataset and a validation dataset: this is known as cross-validation. These repeated partitions can be done in various ways, such as dividing into 2 equal datasets and using them as training/validation, and then validation/training, or repeatedly selecting a random subset as a validation dataset[citation needed]. To validate the model performance, sometimes an additional test dataset that was held out from cross-validation is used.

Cross-validation doesn't work in situations where you can't shuffle your data, most notably in time-series.

Hierarchical classification[edit]

Another example of parameter adjustment is hierarchical classification (sometimes referred to as instance space decomposition [11]), which splits a complete multi-class problem into a set of smaller classification problems. It serves for learning more accurate concepts due to simpler classification boundaries in subtasks and individual feature selection procedures for subtasks. When doing classification decomposition, the central choice is the order of combination of smaller classification steps, called the classification path. Depending on the application, it can be derived from the confusion matrix and, uncovering the reasons for typical errors and finding ways to prevent the system make those in the future. For example,[12] on the validation set one can see which classes are most frequently mutually confused by the system and then the instance space decomposition is done as follows: firstly, the classification is done among well recognizable classes, and the difficult to separate classes are treated as a single joint class, and finally, as a second classification step the joint class is classified into the two initially mutually confused classes.

See also[edit]

References[edit]

  1. ^ Ron Kohavi; Foster Provost (1998). "Glossary of terms". Machine Learning. 30: 271–274.
  2. ^ Machine learning and pattern recognition "can be viewed as two facets of the same field."
  3. ^ a b James, Gareth (2013). An Introduction to Statistical Learning: with Applications in R. Springer. p. 176. ISBN 978-1461471370.
  4. ^ a b Ripley, Brian (1996). Pattern Recognition and Neural Networks. Cambridge University Press. p. 354. ISBN 978-0521717700.
  5. ^ a b Brownlee, Jason (2017-07-13). "What is the Difference Between Test and Validation Datasets?". Retrieved 12 October 2017.
  6. ^ a b Prechelt, Lutz; Geneviève B. Orr (2012-01-01). "Early Stopping — But When?". In Grégoire Montavon; Klaus-Robert Müller. Neural Networks: Tricks of the Trade. Lecture Notes in Computer Science. Springer Berlin Heidelberg. pp. 53–67. doi:10.1007/978-3-642-35289-8_5. ISBN 978-3-642-35289-8.
  7. ^ a b c Ripley, B.D. (1996) Pattern Recognition and Neural Networks, Cambridge: Cambridge University Press, p. 354
  8. ^ a b c d "Subject: What are the population, sample, training set, design set, validation set, and test set?", Neural Network FAQ, part 1 of 7: Introduction (txt), comp.ai.neural-nets, Sarle, W.S., ed. (1997, last modified 2002-05-17)
  9. ^ Bishop, C.M. (1995), Neural Networks for Pattern Recognition, Oxford: Oxford University Press, p. 372
  10. ^ Kohavi, Ron (2001-03-03). "A Study of Cross-Validation and Bootstrap for Accuracy Estimation and Model Selection". 14.
  11. ^ Cohen S, Rokach L., Maimon O. Decision-tree instance-space decomposition with grouped gain-ratio In J. Information Sciences, vol. 177, issue 17, pp. 3592–3612. Elsevier. 2007.
  12. ^ Sidorova, J., Badia, T. "ESEDA: tool for enhanced speech emotion detection and analysis". The 4th International Conference on Automated Solutions for Cross Media Content and Multi-Channel Distribution (AXMEDIS 2008). Florence, November, 17-19, pp. 257–260. IEEE press.

External links[edit]

Retrieved from "https://en.wikipedia.org/w/index.php?title=Training,_validation,_and_test_sets&oldid=875589895"