Monoclinic crystal system
This article may be too technical for most readers to understand. Please help improve it to make it understandable to non-experts, without removing the technical details. (July 2011) (Learn how and when to remove this template message) |

In crystallography, the monoclinic crystal system is one of the 7 crystal systems. A crystal system is described by three vectors. In the monoclinic system, the crystal is described by vectors of unequal lengths, as in the orthorhombic system. They form a rectangular prism with a parallelogram as its base. Hence two vectors are perpendicular (meet at right angles), while the third vector meets the other two at an angle other than 90°.
Contents
Bravais lattices[edit]
Two-dimensional[edit]
There is only one monoclinic Bravais lattice in two dimensions: the oblique lattice.
Three-dimensional[edit]
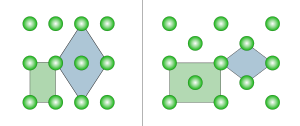
Two monoclinic Bravais lattices exist: the primitive monoclinic and the base-centered monoclinic lattices.
| Bravais lattice | Primitive monoclinic |
Base-centered monoclinic |
|---|---|---|
| Pearson symbol | mP | mS |
| Standard unit cell | 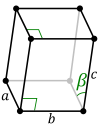
|

|
| Oblique rhombic prism unit cell |
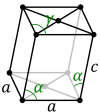
|

|
In the monoclinic system there is a rarely used second choice of crystal axes that results in a unit cell with the shape of an oblique rhombic prism;[1] it can be constructed because the rectangular two-dimensional base layer can also be described with rhombic axes. In this axis setting, the primitive and base-centered lattices swap in centering type.
Crystal classes[edit]
The table below organizes the space groups of the monoclinic crystal system by crystal class. It lists the International Tables for Crystallography space group numbers,[2] followed by the crystal class name, its point group in Schoenflies notation, Hermann–Mauguin (international) notation, orbifold notation, and Coxeter notation, type descriptors, mineral examples, and the notation for the space groups.
| # | Point group | Type | Example | Space groups | |||||
|---|---|---|---|---|---|---|---|---|---|
| Name[3] | Schön. | Intl | Orb. | Cox. | Primitive | Base-centered | |||
| 3–5 | Sphenoidal | C2 | 2 | 22 | [2]+ | enantiomorphic polar | halotrichite | P2, P21 | C2 |
| 6–9 | Domatic | Cs (C1h) | m | *11 | [ ] | polar | hilgardite | Pm, Pc | Cm, Cc |
| 10–12 | Prismatic | C2h | 2/m | 2* | [2,2+] | centrosymmetric | gypsum | P2/m, P21/m | C2/m |
| 13–15 | P2/c, P21/c | C2/c | |||||||
Sphenoidal is also monoclinic hemimorphic; Domatic is also monoclinic hemihedral; Prismatic is also monoclinic normal.
The three monoclinic hemimorphic space groups are as follows:
- a prism with as cross-section wallpaper group p2
- ditto with screw axes instead of axes
- ditto with screw axes as well as axes, parallel, in between; in this case an additional translation vector is one half of a translation vector in the base plane plus one half of a perpendicular vector between the base planes.
The four monoclinic hemihedral space groups include
- those with pure reflection at the base of the prism and halfway
- those with glide planes instead of pure reflection planes; the glide is one half of a translation vector in the base plane
- those with both in between each other; in this case an additional translation vector is this glide plus one half of a perpendicular vector between the base planes.
See also[edit]
References[edit]
- ^ See Hahn (2002), p. 746, row mC, column Primitive, where the cell parameters are given as a1 = a2, α = β
- ^ Prince, E., ed. (2006). International Tables for Crystallography. International Union of Crystallography. doi:10.1107/97809553602060000001. ISBN 978-1-4020-4969-9.
- ^ "The 32 crystal classes". Retrieved 2018-06-19.
Further reading[edit]
- Hurlbut, Cornelius S.; Klein, Cornelis (1985). Manual of Mineralogy (20th ed.). pp. 69–73. ISBN 0-471-80580-7.
- Hahn, Theo, ed. (2002). International Tables for Crystallography, Volume A: Space Group Symmetry. A (5th ed.). Berlin, New York: Springer-Verlag. doi:10.1107/97809553602060000100. ISBN 978-0-7923-6590-7.