Kirchhoff-törvények
A Kirchhoff-törvények a villamosságtanban a töltés és az energia megmaradását tárgyalják. Először Gustav Kirchhoff mondta ki őket 1845-ben. Mindkét törvény közvetlenül levezethető a Maxwell-egyenletekből, de Kirchhoff még Ohm törvényeinek általánosítását használta fel.
Egy tetszőlegesen bonyolult villamos hálózat (áramkör) elemeire egyenként alkalmazható az Ohm-törvény, hiszen az összetartozó áram, feszültség és ellenállás mennyiségek közötti kapcsolatot mutatja. Viszont a több elemből álló hálózatnál a Kirchhoff-törvények nyújtanak segítséget, amelyek leegyszerűsíthetik a számítási műveleteket. Bonyolultabb áramkörök esetén a Kirchhoff egyenletrendszerek megoldása rendkívül hosszadalmas, ezért célszerűbb a Norton-tétel, Thévenin-tétel, Millman-tétel, vagy a szuperpozíció tételének alkalmazása.
Tartalomjegyzék
A csomóponti törvény[szerkesztés]
Kirchhoff I. törvénye.
A csomóponti törvény párhuzamos (elágazó) áramkörökre vonatkozik. Az elágazásnál csomópont keletkezik. A törvény értelmében a csomópontba befolyó áramok összege megegyezik az onnan elfolyó áramok összegével. A törvény alapja az, hogy egy villamos hálózat csomópontjaiban nincs töltésfelhalmozódás (forrásmentes hely).
Az ábrán a csomópontot egy befeketített kör jelöli. A csomópont egyben az elektromos kötés helyét is jelöli.
A csomópontnak létezik még egy fontos jellemzője, az, hogy elektromos potenciállal rendelkezik. Ez a potenciál egy másik csomóponthoz képest mérhető, nagysága függ az összekötő elem(ek) ellenállás-értékétől, és az átfolyó áram nagyságától. A potenciálkülönbség átfolyó áramot hoz létre egy ellenálláson, de azt is mondhatjuk, hogy az átfolyó áram hatására jön létre az ellenállás két végpontja között potenciálkülönbség.
A huroktörvény[szerkesztés]
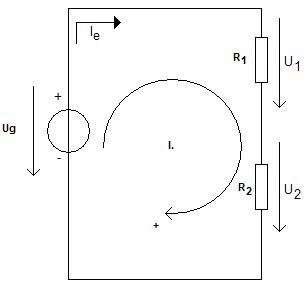
Kirchhoff II. törvénye.
Sorosan kapcsolt áramköri elemekre vonatkozik. A törvény értelmében bármely zárt hurokban a feszültségek előjeles összege nulla.
Az előjel megállapítása úgy történik, hogy egy tetszőleges irányítású "körüljárási irányt" veszünk fel. A körüljárási irányt egy be nem záródó körvonal végén a nyíl jelzi. Ha az áramkör csak egy hurokból áll, a kör középpontjába írt "+" mutatja, hogy az ilyen irányú feszültségeket tekintjük pozitív előjelűnek (azok a feszültségek pedig, melyek iránya a körüljárási iránnyal ellentétes, negatív előjelűek). Ha az áramkör több hurokból áll, a kör középpontjába a hurok sorszáma kerül (az ábrán I.). Zárt hurokban a feszültségforrások összege megegyezik a feszültségesések összegével.
Az egyesített Kirchhoff-törvény[szerkesztés]
Mivel mindkét törvény mindenféle hálózatra igaz, bátran lehet alkalmazni őket ismeretlen feszültségek és/vagy áramok kiszámítására. A most megismertetett két módszerrel bármilyen, tetszőlegesen bonyolult villamos hálózatot ki tudunk számítani, feltéve, ha adottak a megfelelő számú adatok (adatok alatt feszültségek, áramok, ellenállások értékei értendők).
Csak annyit kell tennünk, hogy minden hurokra és minden csomópontra felírjuk a törvényszerűségeket, majd az „ahány ismeretlen, annyi egyenlet” módszerrel az összes ismeretlen feszültséget és áramot ki tudjuk számolni.
Példák:
a)
Vizsgáljuk meg először az I. hurokegyenletet!
I. – Ug1 + UR1 + UR2 = 0
A nem aktív elemek feszültségeit helyettesítsük be az Ohm-törvényből levezethető
U = I * R kifejezéssel.
Így:
I. – Ug1 + I1,2 * R1+ I1,2 * R2= 0
Az egyenlet egy ismeretlent tartalmaz, a megoldása:
I1,2=Ug1/(R1+R2)
b)
Vizsgáljuk most a II. hurokegyenletet!
II. - UR2 - UR1 + UR3 + UR4= 0
A nem aktív elemek feszültségeit ismét helyettesítsük be az Ohm-törvényből levezethető U=I*R kifejezéssel.
Így:
II. - I1,2 * R1 - I1,2 * R2 + I3,4 * R3 + I3,4 * R4= 0
Az egyenlet két ismeretlent tartalmaz (I1,2 és I3,4), de az I1,2 áram az a) pontból behelyettesíthető, így az I3,4 áram meghatározható:
I3,4=I1,2(R1+R2)/(R3+R4)
c)
A csomóponti egyenletből
A: Ie - I1,2 - I3,4
meghatározható az eredő áram:
Ie=I1,2 + I3,4
d)
Az Ohm-törvényből meghatározható az eredő ellenállás:
Re=Ug1 / Ie
valamint a részfeszültségek:
UR1=I1,2 * R1
UR2=I1,2 * R2
UR3=I3,4 * R3
UR4=I3,4 * R4