Test functions for optimization
In applied mathematics, test functions, known as artificial landscapes, are useful to evaluate characteristics of optimization algorithms, such as:
- Convergence rate.
- Precision.
- Robustness.
- General performance.
Here some test functions are presented with the aim of giving an idea about the different situations that optimization algorithms have to face when coping with these kinds of problems. In the first part, some objective functions for single-objective optimization cases are presented. In the second part, test functions with their respective Pareto fronts for multi-objective optimization problems (MOP) are given.
The artificial landscapes presented herein for single-objective optimization problems are taken from Bäck,[1] Haupt et al.[2] and from Rody Oldenhuis software.[3] Given the number of problems (55 in total), just a few are presented here. The complete list of test functions is found on the Mathworks website.[4]
The test functions used to evaluate the algorithms for MOP were taken from Deb,[5] Binh et al.[6] and Binh.[7] You can download the software developed by Deb,[8] which implements the NSGA-II procedure with GAs, or the program posted on Internet,[9] which implements the NSGA-II procedure with ES.
Just a general form of the equation, a plot of the objective function, boundaries of the object variables and the coordinates of global minima are given herein.
Contents
Test functions for single-objective optimization[edit]
| Name | Plot | Formula | Global minimum | Search domain |
|---|---|---|---|---|
| Rastrigin function | 
|
|
||
| Ackley function | 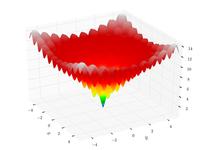
|
|
||
| Sphere function | 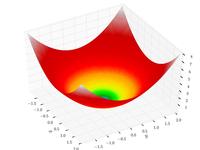
|
, | ||
| Rosenbrock function | 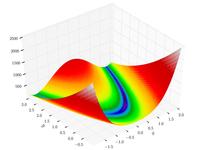
|
, | ||
| Beale function | 
|
|
||
| Goldstein–Price function | 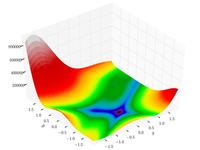
|
|
||
| Booth function | 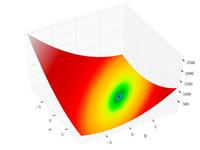
|
|||
| Bukin function N.6 | 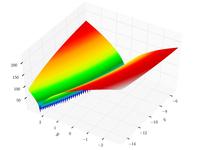
|
, | ||
| Matyas function | 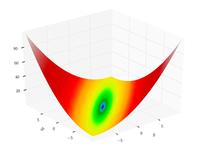
|
|||
| Lévi function N.13 | 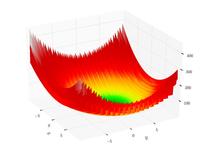
|
|
||
| Himmelblau's function | 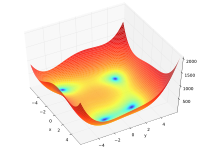
|
|||
| Three-hump camel function | 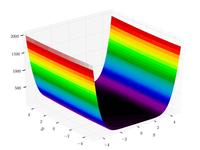
|
|||
| Easom function | 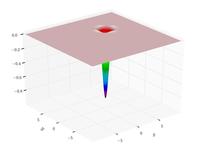
|
|||
| Cross-in-tray function | 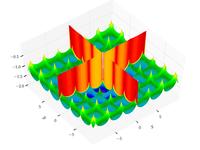
|
|||
| Eggholder function [10] | 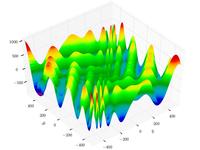
|
|||
| Hölder table function | 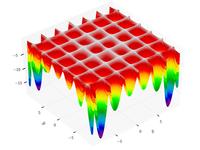
|
|||
| McCormick function | 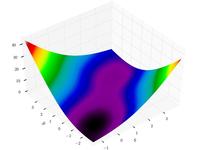
|
, | ||
| Schaffer function N. 2 | 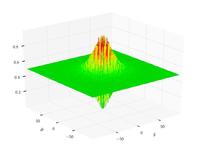
|
|||
| Schaffer function N. 4 | 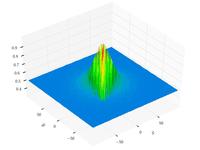
|
|||
| Styblinski–Tang function | 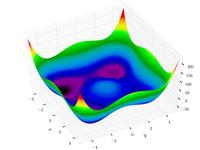
|
, .. |
Test functions for constrained optimization[edit]
| Name | Plot | Formula | Global minimum | Search domain |
|---|---|---|---|---|
| Rosenbrock function constrained with a cubic and a line[11] | 
|
,
subjected to: |
, | |
| Rosenbrock function constrained to a disk[12] | 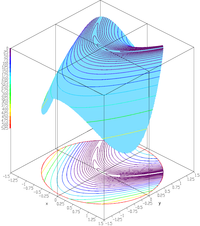
|
,
subjected to: |
, | |
| Mishra's Bird function - constrained[13][14] | 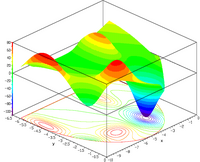
|
,
subjected to: |
, | |
| Townsend function (modified)[15] | 
|
,
subjected to: where: t = Atan2(x,y) |
, | |
| Simionescu function[16] | 
|
,
subjected to: |
Test functions for multi-objective optimization[edit]
| Name | Plot | Functions | Constraints | Search domain |
|---|---|---|---|---|
| Binh and Korn function: | 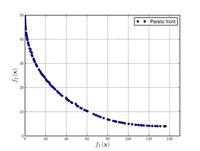
|
, | ||
| Chakong and Haimes function: | 
|
|||
| Fonseca–Fleming function:[17] | 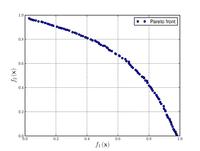
|
, | ||
| Test function 4:[7] | ![Test function 4.[7]](http://upload.wikimedia.org/wikipedia/commons/thumb/3/3c/Test_function_4_-_Binh.pdf/page1-200px-Test_function_4_-_Binh.pdf.jpg)
|
|||
| Kursawe function:[18] | 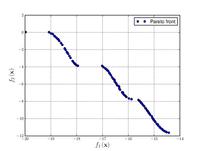
|
, . | ||
| Schaffer function N. 1:[19] | 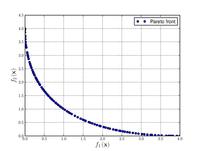
|
. Values of from to have been used successfully. Higher values of increase the difficulty of the problem. | ||
| Schaffer function N. 2: | 
|
. | ||
| Poloni's two objective function: | 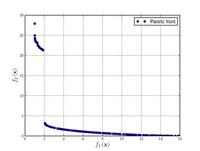
|
|
||
| Zitzler–Deb–Thiele's function N. 1: | 
|
, . | ||
| Zitzler–Deb–Thiele's function N. 2: | 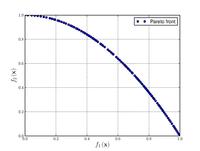
|
, . | ||
| Zitzler–Deb–Thiele's function N. 3: | 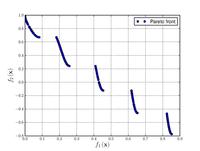
|
, . | ||
| Zitzler–Deb–Thiele's function N. 4: | 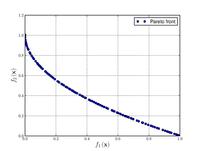
|
, , | ||
| Zitzler–Deb–Thiele's function N. 6: | 
|
, . | ||
| Osyczka and Kundu function: | 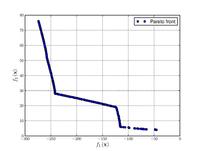
|
, , . | ||
| CTP1 function (2 variables):[5] | ![CTP1 function (2 variables).[5]](http://upload.wikimedia.org/wikipedia/commons/thumb/d/d4/CTP1_function_(2_variables).pdf/page1-200px-CTP1_function_(2_variables).pdf.jpg)
|
. | ||
| Constr-Ex problem:[5] | ![Constr-Ex problem.[5]](http://upload.wikimedia.org/wikipedia/commons/thumb/6/6f/Constr-Ex_problem.pdf/page1-200px-Constr-Ex_problem.pdf.jpg)
|
, | ||
| Viennet function: | 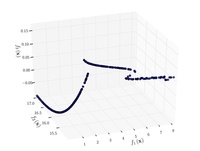
|
. |
See also[edit]
| Wikimedia Commons has media related to Test functions (mathematical optimization). |
References[edit]
- ^ Bäck, Thomas (1995). Evolutionary algorithms in theory and practice : evolution strategies, evolutionary programming, genetic algorithms. Oxford: Oxford University Press. p. 328. ISBN 0-19-509971-0.
- ^ Haupt, Randy L. Haupt, Sue Ellen (2004). Practical genetic algorithms with CD-Rom (2nd ed.). New York: J. Wiley. ISBN 0-471-45565-2.
- ^ Oldenhuis, Rody. "Many test functions for global optimizers". Mathworks. Retrieved 1 November 2012.
- ^ Ortiz, Gilberto A. "Evolution Strategies (ES)". Mathworks. Retrieved 1 November 2012.
- ^ a b c d e Deb, Kalyanmoy (2002) Multiobjective optimization using evolutionary algorithms (Repr. ed.). Chichester [u.a.]: Wiley. ISBN 0-471-87339-X.
- ^ Binh T. and Korn U. (1997) MOBES: A Multiobjective Evolution Strategy for Constrained Optimization Problems. In: Proceedings of the Third International Conference on Genetic Algorithms. Czech Republic. pp. 176–182
- ^ a b c Binh T. (1999) A multiobjective evolutionary algorithm. The study cases. Technical report. Institute for Automation and Communication. Barleben, Germany
- ^ Deb K. (2011) Software for multi-objective NSGA-II code in C. Available at URL:http://www.iitk.ac.in/kangal/codes.shtml. Revision 1.1.6
- ^ Ortiz, Gilberto A. "Multi-objective optimization using ES as Evolutionary Algorithm". Mathworks. Retrieved 1 November 2012.
- ^ Vanaret C., Gotteland J-B., Durand N., Alliot J-M. (2014) Certified Global Minima for a Benchmark of Difficult Optimization Problems. Technical report. Ecole Nationale de l'Aviation Civile. Toulouse, France.
- ^ Simionescu, P.A.; Beale, D. (September 29 – October 2, 2002). New Concepts in Graphic Visualization of Objective Functions (PDF). ASME 2002 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. Montreal, Canada. pp. 891–897. Retrieved 7 January 2017.
- ^ "Solve a Constrained Nonlinear Problem - MATLAB & Simulink". www.mathworks.com. Retrieved 2017-08-29.
- ^ "Bird Problem (Constrained) | Phoenix Integration". wayback.archive.org. Archived from the original on 2016-12-29. Retrieved 2017-08-29.CS1 maint: BOT: original-url status unknown (link)
- ^ Mishra, Sudhanshu (2006). "Some new test functions for global optimization and performance of repulsive particle swarm method". MPRA Paper.
- ^ Townsend, Alex (January 2014). "Constrained optimization in Chebfun". chebfun.org. Retrieved 2017-08-29.
- ^ Simionescu, P.A. (2014). Computer Aided Graphing and Simulation Tools for AutoCAD Users (1st ed.). Boca Raton, FL: CRC Press. ISBN 978-1-4822-5290-3.
- ^ Fonseca, C. M.; Fleming, P. J. (1995). "An Overview of Evolutionary Algorithms in Multiobjective Optimization". Evol Comput. 3 (1): 1–16. doi:10.1162/evco.1995.3.1.1.
- ^ F. Kursawe, “A variant of evolution strategies for vector optimization,” in PPSN I, Vol 496 Lect Notes in Comput Sc. Springer-Verlag, 1991, pp. 193–197.
- ^ Schaffer, J. David (1984). Some experiments in machine learning using vector evaluated genetic algorithms (artificial intelligence, optimization, adaptation, pattern recognition) (PhD). Vanderbilt University. OCLC 20004572.
External links[edit]
- Virtual Library of Simulation Experiments: Test Functions and Datasets
- Benchmarkfcns - Categorized collection of optimization benchmark functions and source code
- Test Functions Index - with an estimate of "hardness" of the problem
- Benchmark functions - Categorized list
- Global Optimization Test Problems - Constrained and unconstrained
- DEAP Benchmarks
![f(\mathbf {x} )=An+\sum _{i=1}^{n}\left[x_{i}^{2}-A\cos(2\pi x_{i})\right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/1aa1c38ee739ca9cf4582867d74d469df4676cbc)



![{\displaystyle f(x,y)=-20\exp \left[-0.2{\sqrt {0.5\left(x^{2}+y^{2}\right)}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7f00d1325d65d088f8ae6a96137e62021107921d)
![{\displaystyle -\exp \left[0.5\left(\cos 2\pi x+\cos 2\pi y\right)\right]+e+20}](https://wikimedia.org/api/rest_v1/media/math/render/svg/565ef43958a50fb0ef473bdd46e30bfc725604a7)






![{\displaystyle f({\boldsymbol {x}})=\sum _{i=1}^{n-1}\left[100\left(x_{i+1}-x_{i}^{2}\right)^{2}+\left(1-x_{i}\right)^{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/64863353dcdea2f0ed049cec3aea0a4284d4916a)





![{\displaystyle f(x,y)=\left[1+\left(x+y+1\right)^{2}\left(19-14x+3x^{2}-14y+6xy+3y^{2}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2d020ed324ff07759faf17591157771b0e2cdf07)
![{\displaystyle \left[30+\left(2x-3y\right)^{2}\left(18-32x+12x^{2}+48y-36xy+27y^{2}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/32e562da4f3219f9d66e059441c59e1d299e8557)



















![{\displaystyle f(x,y)=-0.0001\left[\left|\sin x\sin y\exp \left(\left|100-{\frac {\sqrt {x^{2}+y^{2}}}{\pi }}\right|\right)\right|+1\right]^{0.1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d591ae9bcf2feae162cd00398d78bb6870c82946)










![{\displaystyle f(x,y)=0.5+{\frac {\sin ^{2}\left(x^{2}-y^{2}\right)-0.5}{\left[1+0.001\left(x^{2}+y^{2}\right)\right]^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/995008c6f10a14b44dac568cc544efb7d5ddd631)
![{\displaystyle f(x,y)=0.5+{\frac {\cos ^{2}\left[\sin \left(\left|x^{2}-y^{2}\right|\right)\right]-0.5}{\left[1+0.001\left(x^{2}+y^{2}\right)\right]^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2458c352c0c0524648d8ef713bcea4e80df32fd8)











![{\displaystyle f(x,y)=\sin(y)e^{\left[(1-\cos x)^{2}\right]}+\cos(x)e^{\left[(1-\sin y)^{2}\right]}+(x-y)^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7987d4a794d861e7ccd0795265841d3ca172cfae)




![{\displaystyle f(x,y)=-[\cos((x-0.1)y)]^{2}-x\sin(3x+y)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8dac25f97d0b720512d72c313000d5fb5c7d033a)
![{\displaystyle x^{2}+y^{2}<\left[2\cos t-{\frac {1}{2}}\cos 2t-{\frac {1}{4}}\cos 3t-{\frac {1}{8}}\cos 4t\right]^{2}+[2\sin t]^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/57168b192e685c6144e3a9527b12087ac7cb11b4)




![{\displaystyle x^{2}+y^{2}\leq \left[r_{T}+r_{S}\cos \left(n\arctan {\frac {x}{y}}\right)\right]^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1fc42adcc2095ed0c0214a74799db7ee2fac9923)










![{\displaystyle {\text{Minimize}}={\begin{cases}f_{1}\left({\boldsymbol {x}}\right)=1-\exp \left[-\sum _{i=1}^{n}\left(x_{i}-{\frac {1}{\sqrt {n}}}\right)^{2}\right]\\f_{2}\left({\boldsymbol {x}}\right)=1-\exp \left[-\sum _{i=1}^{n}\left(x_{i}+{\frac {1}{\sqrt {n}}}\right)^{2}\right]\\\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3113203c5d455e0e1e6397d57094e80e527b34ba)




![{\displaystyle {\text{Minimize}}={\begin{cases}f_{1}\left({\boldsymbol {x}}\right)=\sum _{i=1}^{2}\left[-10\exp \left(-0.2{\sqrt {x_{i}^{2}+x_{i+1}^{2}}}\right)\right]\\&\\f_{2}\left({\boldsymbol {x}}\right)=\sum _{i=1}^{3}\left[\left|x_{i}\right|^{0.8}+5\sin \left(x_{i}^{3}\right)\right]\\\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aeb9856144d9869aae4254892ece0fe894dfc152)








![{\displaystyle {\text{Minimize}}={\begin{cases}f_{1}\left(x,y\right)=\left[1+\left(A_{1}-B_{1}\left(x,y\right)\right)^{2}+\left(A_{2}-B_{2}\left(x,y\right)\right)^{2}\right]\\f_{2}\left(x,y\right)=\left(x+3\right)^{2}+\left(y+1\right)^{2}\\\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ee5df22af124899c1e268325017ea64e517b51e)










![{\displaystyle {\text{Minimize}}={\begin{cases}f_{1}\left({\boldsymbol {x}}\right)=1-\exp \left(-4x_{1}\right)\sin ^{6}\left(6\pi x_{1}\right)\\f_{2}\left({\boldsymbol {x}}\right)=g\left({\boldsymbol {x}}\right)h\left(f_{1}\left({\boldsymbol {x}}\right),g\left({\boldsymbol {x}}\right)\right)\\g\left({\boldsymbol {x}}\right)=1+9\left[{\frac {\sum _{i=2}^{10}x_{i}}{9}}\right]^{0.25}\\h\left(f_{1}\left({\boldsymbol {x}}\right),g\left({\boldsymbol {x}}\right)\right)=1-\left({\frac {f_{1}\left({\boldsymbol {x}}\right)}{g\left({\boldsymbol {x}}\right)}}\right)^{2}\\\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f03bdd2b0c7a5af33b0a0fc385f9a9c021635d6e)














