Piros-fekete fa

Piros-fekete fa
Típus	Fa
Komplexitás (O jelöléssel)
Tárigény	O(n)
Beszúrás	O(log n)
Keresés	O(log n)
Törlés	O(log n)

A számítástudományban a piros-fekete fa alatt egy önkiegyensúlyozó bináris keresőfát értünk. A szerkezete összetett, de a gyakorlatban hatékony, hiszen a keresés, beszúrás és törlés lépésszáma a legrosszabb esetben is O(log n), ahol n a fában levő elemek száma.

Tulajdonságai

Egy piros-fekete fa

A piros-fekete fa egy olyan bináris keresőfa, melyben minden csúcsot kiszínezünk piros vagy fekete színnel. A bináris keresőfa tulajdonságain kívül (minden csúcs bal oldali részfájában csak kisebb (<), jobb oldali részfájában csak nagyobb vagy egyenlő (nem kisebb, >=) elemek helyezkednek el) a piros-fekete fákkal szemben a következő követelményeket támasztjuk:

1. Egy csúcs vagy fekete vagy piros.
2. A fa gyökere fekete.
3. Minden levél a fa gyökerével egyszínű. (A 2. szabályból adódóan tehát minden levél fekete)
4. Egy piros csúcs mindkét leszármazottja fekete.
5. Minden csúcsból a belőle leszármazó levelekbe vezető egyszerű utakon ugyanannyi fekete csúcsot érintünk.

Ezekből a követelményekből származik a piros-fekete fák egy fontos tulajdonsága: A gyökérelemtől a hozzá legközelebbi levélbe vezető út hosszának legfeljebb kétszerese a gyökértől a hozzá legtávolabbi levélbe vezető út hossza, amelyből következik, hogy a fa önkiegyensúlyozó.

Ennek a tulajdonságnak a belátásához elegendő a 4. és 5. követelményt megvizsgálni. Egy F piros-fekete fában legyen az 5. szabályban meghatározott fekete csúcsok száma N - ekkor tehát a legrövidebb út a gyökértől a levélig összesen N csúcsból áll, melyből mind fekete. Az út hossza növelhető piros csúcsok beillesztésével, de a 4. szabály miatt nem szúrható be egymás után több, mint 1 piros csúcs, azaz legfeljebb N darab piros csúcsot illeszthetünk be. Így a lehető leghosszabb út a gyökértől egy levélig 2N csúcsból áll, melyek felváltva pirosak és feketék.

Az egyszerűség kedvéért a piros-fekete fákban csak a belső csúcsok tartalmaznak hasznos adatot, a levelek pedig adatot nem tartalmazó fekete csúcsok - ennek hiányában lehetséges lenne, hogy egy belső csúcsnak csak egy leszármazottja legyen, amely bonyolítaná a fa követelményrendszerét. Ezeket az adatot nem tartalmazó leveleket gyakran nem ábrázoljuk a fa szemléltetése során, így egy olyan fát kapunk, ami látszólag ellentmond a követelményeknek, de a gyakorlatban nem. Mivel az összes ilyen levél fekete, az 5. szabály triviálisan nem sérül.

Műveletek

A piros-fekete fákkal végezhető műveletek megegyeznek a bináris keresőfákkal végezhető műveletekkel, azok módosításra nem szorulnak, csupán kiegészítésre, mivel egy újabb csúcs beszúrása vagy egy már létező elem törlése sértheti a piros-fekete fa tulajdonságot. Ennek a helyreállításához nincs szükség több, mint O(log n) átszínezésre és három (beszúrás esetén kettő) faforgatásra, így a beszúrás és törlés lépésszáma, a bináris keresőfához hasonlóan, O(log n).

Keresés

A piros-fekete fában a keresés teljes mértékben megegyezik a bináris keresőfában való kereséssel. A gyökérelemtől kiindulva balra haladunk, ha a keresett elem kisebb mint a jelenlegi elem, jobbra, ha nagyobb. Amennyiben egy adatot nem tartalmazó levélhez érünk mielőtt megtaláltuk volna az elemet, a fa nem tartalmazza a keresett elemet.

Ezt megvalósító rekurzív C példakód:

int keres(int elem, struct faelem* n)
{
  if (n->elem == elem)
    return 1;
  if (n->elem < elem && n->jobb)
  {
    return keres(elem, n->jobb);
  }
  else if (n->elem > elem && n->bal)
  {
    return keres(elem, n->bal);
  }
  else return 0;
}

Megjegyzés: A kódban feltételezzük, hogy az adatot nem tartalmazó leveleket egy null-ra mutató pointer jelöli.

Beszúrás

A fába való beszúrás során először ugyanazokat a lépéseket végezzük el, mint egy bináris keresőfában. Az új elemet pirosra színezzük, és két új levéllel hozzuk létre, majd egy (adatot nem tartalmazó) levél helyére szúrjuk be.

A további lépéseket a környező elemek színe határozza meg. A következő lépésekben N jelöli a jelenleg vizsgált elemet, P a szülőelemet, G a nagyszülő (szülő elem szüleje) elemet, U pedig az N elem "nagybátyját" (azaz G másik (nem P) leszármazottját). Az egyes lépésekben az elemeknek a viszonylagos elhelyezkedése megváltozhat, ekkor a betűk ugyanazt az elemet jelölik, mint a lépés elején. Az ábrákon jelölt színek az adott lépésben történt feltevésekből, illetve azok következmenyeiből adódnak.

A lépésekhez példaként C kód is tartozik. A nagyszülő és nagybáty elemeket a következő függvények segítségével keressük meg:

struct faelem* nagyszulo(struct faelem* n)
{
  if (n && n->szulo)
  {
    return n->szulo->szulo;
  }
  return NULL;
}

struct faelem* nagybaty(struct faelem* n)
{
  struct faelem* g = nagyszulo(n);
  if (g)
  {
    if (n->szulo == g->bal)
    {
      return g->jobb;
    } else {
      return g->bal;
    }
  }
  return NULL;
}

1. lépés: Ha a jelenlegi N elem a fa gyökere, azt átszínezzük feketére, hogy kielégítse a 2. követelményt. Ezzel az összes úton eggyel több fekete csúcs jelenik meg, így az 5. követelmény nem sérül. Amennyiben ez az elem valóban a gyökér, további lépésekre nincs szükség.

void beszur_1(struct faelem* n)
{
  if (!n->szulo)
  {
    n->szin = FEKETE;
  } else {
    beszur_2(n);
  }
}

2. lépés: Ha a jelenlegi elem P szüleje fekete, nem sérül a 4. követelmény - így a fa egy érvényes piros-fekete fa. Amennyiben ez fennáll, további lépésekre nincs szükség.

void beszur_2(struct faelem* n)
{
  if (n->szulo->szin == FEKETE)
  {
    return;
  } else {
    beszur_3(n);
  }
}

A 3. lépés

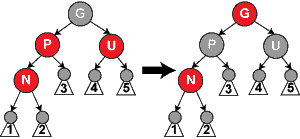
3. lépés: Ha a jelenlegi elem P szüleje és U nagybátyja is piros, mindkettőt átszínezhetjük feketére, a G nagyszülőt pedig pirosra, így nem változik az egyes utakon a fekete csúcsok száma, mivel minden út amely P vagy U csúcsokon áthalad triviálisan áthalad G csúcson is. Az N szüleje most már fekete, így (mivel N piros) nem sérti a 4. követelményt. Ekkor viszont G sértheti a 2. (a gyökér fekete) illetve 4. (piros elem gyerekei feketék) szabályt, az utóbbit abban az esetben, ha G szüleje is piros. Ennek áthidalására ugyanezeket a lépéseket rekurzívan elvégezzük G-re is. Ha a feltételek teljesültek, az N környezete most már a követelményeknek megfelel, amennyiben nem, továbbhaladunk a 4. lépésre. Ebből is következik az, hogy O(1) (konstans) faforgatást végzünk, hiszen faforgatás csak a 4. és 5. lépésekben szükséges, ahova beszúrásonként legfeljebb egy elem esetén jutunk el.

void beszur_3(struct faelem* n)
{
  struct faelem* u = nagybaty(n);
  struct faelem* g = nagyszulo(n);
  if (u && u->szin == PIROS)
  {
    u->szin = FEKETE;
    n->szulo->szin = FEKETE;
    g->szin = PIROS;
    beszur_1(g);
  } else {
    beszur_4(n);
  }
}

Megjegyzés: A továbbiakban feltételezzük, hogy P a bal oldali gyereke G-nek. Ha P a jobb oldali gyerek, akkor a 4. és 5. lépés során tekintsük az összes irányt ellentétesen. A kódban mindkét esetre kitérünk.

A 4. lépés

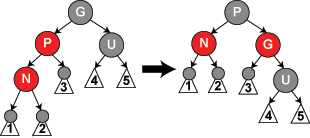
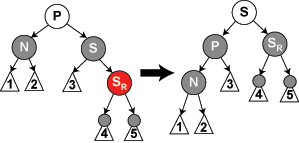
4. lépés: Amennyiben P piros, de U fekete (ezek a feltételek teljesülnek, hiszen ellenőriztük őket a 2. és 3. lépésben), illetve N a jobb oldali gyereke P-nek, P balra forgatásával felcseréljük N és P szerepét. Ekkor néhány út amely eddig nem haladt át N csúcson most már áthalad rajta, és néhány út, amely áthaladt P csúcson most már nem halad át rajta, de ezzel nem sérül az 5. követelmény, mivel mindkét csúcs piros. A 4. követelmény továbbra is sérül, melyet az 5. lépésben oldunk fel.

void beszur_4(struct faelem* n)
{
  struct faelem* g = nagyszulo(n);
  if (n == n->szulo->jobb && g->bal == n->szulo)
  {
    balra_forgat(n->szulo);
    n = n->bal;
  }
  else if (n == n->szulo->bal && g->jobb == n->szulo)
  {
    jobbra_forgat(n->szulo);
    n = n->jobb;
  }
  beszur_5(n);
}

Az 5. lépés

5. lépés: P piros, U fekete és N a P bal oldali gyereke. Ekkor G elemet jobbra forgatjuk, melynek eredményeképpen P most már N és G szüleje. G-ről tudjuk, hogy fekete, különben P nem lehetne piros a 4. szabály következtében. Megcseréljük tehát P és G színét, így P most már fekete, G pedig piros, így a 4. követelmény is teljesül. Az 5. követelmény nem sérül, hiszen azok az utak, amelyek eddig G-n haladtak át most P-n haladnak át, ami ugyanúgy fekete. Azok az utak, amelyek U-n haladnak át most már áthaladnak G-n is, amely piros, tehát a fekete csúcsok száma ugyanannyi marad. Azok az utak, amelyek pedig N-en haladtak át most már eggyel kevesebb piros csúcson haladnak át, tehát a fekete csúcsok száma változatlan.

void beszur_5(struct faelem* n)
{
  struct faelem* g = nagyszulo(n);
  n->szulo->szin = FEKETE;
  g->szin = PIROS;
  if (n == n->szulo->bal && n->szulo == g->bal)
  {
    jobbra_forgat(g);
  }
  else if (n == n->szulo->jobb && n->szulo == g->jobb)
  {
    balra_forgat(g);
  }
}

Törlés

Amennyiben a törlésre kijelölt elemnek két belső (azaz nem levél) leszármazottja van, akkor - a bináris keresőfával megegyező módon - megkeressük vagy az elem bal részfájának legnagyobb elemét, vagy pedig a jobb részfájának a legkisebb elemét, és ezek adattagját kicseréljük. Ezt piros-fekete fában is megtehetjük, hiszen az elem színe nem változott. Így most már a törlendő elem viszont az az elem, amelynek adattagját áthelyeztük, és ennek az elemnek legfeljebb egy belső leszármazottja van; ha az elemnek kettő belső leszármazottja lenne, az nem lehetne az adott részfának se a legnagyobb, se a legkisebb eleme, mivel a keresőfa tulajdonságból adódóan a bal oldali gyereke kisebb, a jobb oldali gyereke pedig nagyobb.

Az algoritmus további lépései során tehát egy olyan elemet törlünk amelynek legfeljebb egy belső leszármazottja van. A továbbiakban M jelöli a törlendő elemet, C pedig M kijelölt leszármazottját - amennyiben létezik belső leszármazottja azt, egyébként pedig tetszőleges leszármazott levelet.

Ekkor négy esetet különböztethetünk meg M és C színét illetően.

M és C piros eset nem állhat fent, hiszen ez ütközik a 4. követelménnyel.

Ha M piros és C fekete, akkor M-et egyszerűen kicserélhetjük C-re. Minden út amelyik eddig M-en áthaladt most csupán eggyel kevesebb piros csúcsot érint, így az 5. szabály nem sérül.

Ha M fekete és C piros, akkor M-et kicseréljük C-re és C-t átfestjük feketére. Ezzel minden út ami eddig áthaladt M-en eggyel kevesebb piros csúcsot érint, tehát az 5. szabály így se sérül.

A legbonyolultabb eset az, amikor M és C is fekete. Ez csak akkor fordulhat elő, ha C levél, mivel ha C egy belső fekete elem, akkor az 5. követelmény sérül, mivel a C irányába haladó utak mentén legalább eggyel több fekete csúcs lenne, mint az M másik leszármazottjában végződő utak mentén, tehát a fa amiből törlünk ekkor nem egy érvényes piros-fekete fa lenne. Ebben az esetben M-et kicseréljük az adatot nem tartalmazó C levélre. A továbbiakban ezt a C elemet jelöljük N-nel. N testvéreleme (azaz N új szülejének másik leszármazottja) S, új szüleje (azaz M régi szüleje) P, S_L a testvérelem (S) bal oldali, S_R pedig a jobb oldali leszármazottja. S biztosan nem levélelem, mivel ha N fekete (amelyet feltételeztünk), akkor P egyik részfája 2 feketemagasságú, tehát triviálisan a másik részfájának is 2 feketemagasságúnak kell lennie, amely nem állhat fent ha S levélelem.

Az egyes lépésekben az elemek viszonylagos helyzete megváltozik, de a jelölések minden lépésben végig ugyanazt az elemet jelölik, amelyet a lépés elején. Az ábrákban a feltételezésekből és azoknak következményeiből adódnak a színezések. Fehér színnel jelöljük azt az elemet, amelynek színét nem tudjuk. A lépések során szükség lesz a testvérelem meghatározására, amelyet a következő függvény végez:

struct faelem* testver(struct node* n)
{
  if (n == n->szulo->bal)
    return n->szulo->jobb;
  else return n->szulo->bal;
}

A fenti lépéseket az alábbi kóddal végezhetjük (az athelyez függvény a fában áthelyezi az első paraméterként kapott elemet a második paraméterként kapott elem helyére):

void torol_egylevel(struct faelem* n)
{
  struct faelem* gyerek = (n->bal) ? n->bal : n->jobb;
  if (gyerek)
  {
    athelyez(gyerek, n);
    gyerek->szin = FEKETE;
  } else {
    torol_1(n);
    if (n->szulo->bal == n)
      n->szulo->bal = NULL;
    else
      n->szulo->jobb = NULL;
  }
  free(n);
}

A korábbi mintára feltételezzük, hogy az adatot nem tartalmazó levelek nem mások, mint NULL-ra mutató pointerek.

Mivel N és M (azaz N eredeti szüleje) is fekete volt, néhány úton csökkent a fekete csúcsok száma - azaz sérült az 5. tulajdonság - tehát a fát újra ki kell egyensúlyoznunk. Ez is több lépésben történik.

1. lépés: Ha N az új gyökérelem, akkor nem kell tennünk semmit, hiszen ekkor a korábbi gyökérelemet töröltük, tehát minden útról eltávolítottunk egy fekete csúcsot.

void torol_1(struct faelem* n)
{
   if (n->szulo)
     torol_2(n);
}

Megjegyzés: A 2., 5. és 6. lépések során feltételezzük, hogy N a bal oldali gyereke P-nek. Amennyiben N a jobb oldali gyerek, az irányok felcserélődnek. A kódrészletek itt is figyelembe veszik ezt.

A 2. lépés

2. lépés: Ha S piros, megcseréljük P és S színét, majd balra forgatjuk P-t. P elem eredetileg fekete színű kellett, hogy legyen, hiszen volt egy piros gyereke. Az 5. követelmény a színcsere miatt nem sérül. A továbbiakban N új testvérét jelöljük S-el.

void torol_2(struct faelem* n)
{
  struct faelem* s = testver(n);
  if (s->szin == PIROS)
  {
    n->szulo->szin = PIROS;
    s->szin = FEKETE;
    if (n == n->szulo->bal)
      balra_forgat(n->szulo);
    else
      jobbra_forgat(n->szulo);
  }
  torol_3(n);
}

A 3. lépés

3. lépés: Ha S, P és S mindkét leszármazottja fekete, akkor egyszerűen átszínezzük S-t pirosra; mivel M törlésekor az összes S-en áthaladó úton eggyel több fekete csúcs lett, mint az N-en áthaladó utakon. Ekkor viszont az 5. követelmény továbbra is sérülhet, hiszen ha P nem gyökérelem, hanem egy nagyobb piros-fekete fa részfája, akkor az összes P csúcson áthaladó út eggyel kevesebb fekete csúcsot érint, mint azok az utak, amelyek más irányba haladnak, tehát ugyanezt a lépéssorozatot elvégezzük P-re, viszont ilyenkor N-re nézve a további lépésekre már nincs szükség.

void torol_3(struct faelem* n)
{
  struct faelem* s = testver(n);
  if (n->szulo->szin == FEKETE && s->szin == FEKETE && s->bal->szin == FEKETE && s->jobb->szin == FEKETE)
  {
    s->szin = PIROS;
    torol_1(n->szulo);
  } else {
    torol_4(n);
  }
}

A 4. lépés

4. lépés: Ha S és leszármazottai feketék, de P piros, akkor egyszerűen felcseréljük P és S színét. Ekkor ugyanabba az állapotba jutunk, mint a 3. lépés során, viszont ekkor nem az S ág feketemagassága csökken eggyel, hanem az N ágé nő, tehát a kitörölt fekete által okozott követelmény sérülést kiküszöböltük, tehát a feltétel fennállása esetén nincs szükség több lépésre.

void torol_4(struct faelem* n)
{
  struct faelem* s = testver(n);
  if (n->szulo->szin == PIROS && s->szin == FEKETE && s->bal->szin == FEKETE && s->jobb->szin == FEKETE)
  {
    n->szulo->szin = FEKETE;
    s->szin = PIROS;
  } else {
    torol_5(n);
  }
}

Az 5. lépés

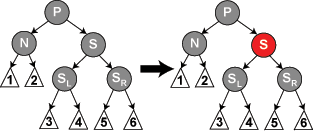
5. lépés: Ha S és P és S_R feketék, de S_L piros és N elem P bal oldali leszármazottja, akkor S elemet jobbra forgatjuk, így S_L lesz S új szüleje. Ezután felcseréljük S és S_L színét. Most már minden úton azonos a fekete csúcsok száma, de az N csúcs új testvére most már egy fekete elem, amelynek a jobb oldali leszármazottja piros, tehát továbblépünk a 6. lépésre.

void torol_5(struct faelem* n)
{
  struct faelem* s = testver(n);
  if (s->szin == FEKETE)
  {
    if (n == n->szulo->bal && s->bal->szin == PIROS && s->jobb->szin == FEKETE)
    {
      s->szin = PIROS;
      s->bal->szin = FEKETE;
      jobbra_forgat(s);
    }
    else if (n == n->szulo->jobb && s->bal->szin == FEKETE && s->jobb->szin == PIROS)
    {
      s->szin = PIROS;
      s->jobb->szin = FEKETE;
      balra_forgat(s);
    }
  }
  torol_6(n);
}

A 6. lépés

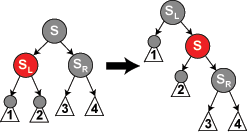
6. lépés: S (az 5. lépésben S_L) tehát fekete, S_R (az 5. lépésben S) piros, N pedig a P bal oldali gyereke. P elemnél ekkor balra forgatjuk a fát, ezután pedig megcseréljük S és P színét és S_R-t feketére festjük. N-nek így most már eggyel több fekete felmenője van, tehát helyreállt az 5. követelmény véglegesen.

void torol_6(struct faelem* n)
{
  struct faelem* s = testver(n);
  s->szin = n->szulo->szin;
  n->szulo->szin = FEKETE;
  if (n == n->szulo->bal)
  {
    s->jobb->szin = FEKETE;
    balra_forgat(n->szulo);
  } else {
    s->bal->szin = FEKETE;
    jobbra_forgat(n->szulo);
  }
}

Az eddigi lépésekben az összes lehetőséget lefedtük és korrigáltuk, tehát a fa ismételten egy érvényes piros-fekete fa.

Források

• Friedl Katalin: Piros-fekete fák (PDF). (Hozzáférés: 2011. december 29.)
• Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, Clifford Stein. 13. fejezet: Piros-fekete fák, Új algoritmusok, 2. kiadás, MIT Press and McGraw-Hill, 273–301. o. (2001). ISBN 0-262-03293-7