Symmetric relation
This article does not cite any sources. (February 2019) (Learn how and when to remove this template message) |
A symmetric relation is a type of binary relation. An example is the relation "is equal to", because if a = b is true then b = a is also true. Formally, a binary relation R over a set X is symmetric if and only if:
If RT represents the converse of R, then R is symmetric if and only if R = RT.
Symmetry, along with reflexivity and transitivity, are the three defining properties of an equivalence relation.
Contents
Examples[edit]
In mathematics[edit]
- "is equal to" (equality) (whereas "is less than" is not symmetric)
- "is comparable to", for elements of a partially ordered set
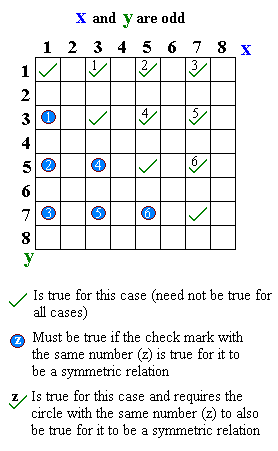
- "... and ... are odd":
Outside mathematics[edit]
- "is married to" (in most legal systems)
- "is a fully biological sibling of"
- "is a homophone of"
Relationship to asymmetric and antisymmetric relations[edit]
By definition, a relation cannot be both symmetric and asymmetric (where if a is related to b, then b cannot be related to a (in the same way)). However, a relation can be neither symmetric nor asymmetric, which is the case for "is less than or equal to" and "preys on").
Symmetric and antisymmetric (where the only way a can be related to b and b be related to a is if a = b) are actually independent of each other, as these examples show.
| Symmetric | Not symmetric | |
| Antisymmetric | equality | "is less than or equal to" |
| Not antisymmetric | congruence in modular arithmetic | "is divisible by", over the set of integers |
| Symmetric | Not symmetric | |
| Antisymmetric | "is the same person as, and is married" | "is the plural of" |
| Not antisymmetric | "is a full biological sibling of" | "preys on" |
Additional aspects[edit]
A symmetric relation that is also transitive and reflexive is an equivalence relation.
One way to conceptualize a symmetric relation in graph theory is that a symmetric relation is an edge, with the edge's two vertices being the two entities so related. Thus, symmetric relations and undirected graphs are combinatorially equivalent objects.