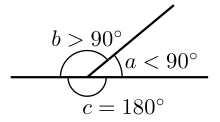Page semi-protected

Geometry

From Wikipedia, the free encyclopedia
Jump to navigation Jump to search
For other uses, see Geometry (disambiguation).

Geometry
Stereographic projection in 3D.svg
Projecting a sphere to a plane.
Geometers
Crystal Clear app 3d.png Geometry portal
An illustration of Desargues' theorem, an important result in Euclidean and projective geometry

Geometry (from the Ancient Greek: γεωμετρία; geo- "earth", -metron "measurement") is a branch of mathematics concerned with questions of shape, size, relative position of figures, and the properties of space. A mathematician who works in the field of geometry is called a geometer.

Geometry arose independently in a number of early cultures as a practical way for dealing with lengths, areas, and volumes. Geometry began to see elements of formal mathematical science emerging in the West as early as the 6th century BC.[1] By the 3rd century BC, geometry was put into an axiomatic form by Euclid, whose treatment, Euclid's Elements, set a standard for many centuries to follow.[2] Geometry arose independently in India, with texts providing rules for geometric constructions appearing as early as the 3rd century BC.[3] Islamic scientists preserved Greek ideas and expanded on them during the Middle Ages.[4] By the early 17th century, geometry had been put on a solid analytic footing by mathematicians such as René Descartes and Pierre de Fermat. Since then, and into modern times, geometry has expanded into non-Euclidean geometry and manifolds, describing spaces that lie beyond the normal range of human experience.[5]

While geometry has evolved significantly throughout the years, there are some general concepts that are more or less fundamental to geometry. These include the concepts of points, lines, planes, surfaces, angles, and curves, as well as the more advanced notions of manifolds and topology or metric.[6]

Geometry has applications to many fields, including art, architecture, physics, as well as to other branches of mathematics.

Overview

Contemporary geometry has many subfields:

History

Main article: History of geometry
A European and an Arab practicing geometry in the 15th century.

The earliest recorded beginnings of geometry can be traced to ancient Mesopotamia and Egypt in the 2nd millennium BC.[8][9] Early geometry was a collection of empirically discovered principles concerning lengths, angles, areas, and volumes, which were developed to meet some practical need in surveying, construction, astronomy, and various crafts. The earliest known texts on geometry are the Egyptian Rhind Papyrus (2000–1800 BC) and Moscow Papyrus (c. 1890 BC), the Babylonian clay tablets such as Plimpton 322 (1900 BC). For example, the Moscow Papyrus gives a formula for calculating the volume of a truncated pyramid, or frustum.[10] Later clay tablets (350–50 BC) demonstrate that Babylonian astronomers implemented trapezoid procedures for computing Jupiter's position and motion within time-velocity space. These geometric procedures anticipated the Oxford Calculators, including the mean speed theorem, by 14 centuries.[11] South of Egypt the ancient Nubians established a system of geometry including early versions of sun clocks.[12][13]

In the 7th century BC, the Greek mathematician Thales of Miletus used geometry to solve problems such as calculating the height of pyramids and the distance of ships from the shore. He is credited with the first use of deductive reasoning applied to geometry, by deriving four corollaries to Thales' Theorem.[1] Pythagoras established the Pythagorean School, which is credited with the first proof of the Pythagorean theorem,[14] though the statement of the theorem has a long history.[15][16] Eudoxus (408–c. 355 BC) developed the method of exhaustion, which allowed the calculation of areas and volumes of curvilinear figures,[17] as well as a theory of ratios that avoided the problem of incommensurable magnitudes, which enabled subsequent geometers to make significant advances. Around 300 BC, geometry was revolutionized by Euclid, whose Elements, widely considered the most successful and influential textbook of all time,[18] introduced mathematical rigor through the axiomatic method and is the earliest example of the format still used in mathematics today, that of definition, axiom, theorem, and proof. Although most of the contents of the Elements were already known, Euclid arranged them into a single, coherent logical framework.[19] The Elements was known to all educated people in the West until the middle of the 20th century and its contents are still taught in geometry classes today.[20] Archimedes (c. 287–212 BC) of Syracuse used the method of exhaustion to calculate the area under the arc of a parabola with the summation of an infinite series, and gave remarkably accurate approximations of Pi.[21] He also studied the spiral bearing his name and obtained formulas for the volumes of surfaces of revolution.

Woman teaching geometry. Illustration at the beginning of a medieval translation of Euclid's Elements, (c. 1310)

Indian mathematicians also made many important contributions in geometry. The Satapatha Brahmana (3rd century BC) contains rules for ritual geometric constructions that are similar to the Sulba Sutras.[3] According to (Hayashi 2005, p. 363), the Śulba Sūtras contain "the earliest extant verbal expression of the Pythagorean Theorem in the world, although it had already been known to the Old Babylonians. They contain lists of Pythagorean triples,[22] which are particular cases of Diophantine equations.[23] In the Bakhshali manuscript, there is a handful of geometric problems (including problems about volumes of irregular solids). The Bakhshali manuscript also "employs a decimal place value system with a dot for zero."[24] Aryabhata's Aryabhatiya (499) includes the computation of areas and volumes. Brahmagupta wrote his astronomical work Brāhma Sphuṭa Siddhānta in 628. Chapter 12, containing 66 Sanskrit verses, was divided into two sections: "basic operations" (including cube roots, fractions, ratio and proportion, and barter) and "practical mathematics" (including mixture, mathematical series, plane figures, stacking bricks, sawing of timber, and piling of grain).[25] In the latter section, he stated his famous theorem on the diagonals of a cyclic quadrilateral. Chapter 12 also included a formula for the area of a cyclic quadrilateral (a generalization of Heron's formula), as well as a complete description of rational triangles (i.e. triangles with rational sides and rational areas).[25]

In the Middle Ages, mathematics in medieval Islam contributed to the development of geometry, especially algebraic geometry.[26][27] Al-Mahani (b. 853) conceived the idea of reducing geometrical problems such as duplicating the cube to problems in algebra.[28] Thābit ibn Qurra (known as Thebit in Latin) (836–901) dealt with arithmetic operations applied to ratios of geometrical quantities, and contributed to the development of analytic geometry.[4] Omar Khayyám (1048–1131) found geometric solutions to cubic equations.[29] The theorems of Ibn al-Haytham (Alhazen), Omar Khayyam and Nasir al-Din al-Tusi on quadrilaterals, including the Lambert quadrilateral and Saccheri quadrilateral, were early results in hyperbolic geometry, and along with their alternative postulates, such as Playfair's axiom, these works had a considerable influence on the development of non-Euclidean geometry among later European geometers, including Witelo (c. 1230–c. 1314), Gersonides (1288–1344), Alfonso, John Wallis, and Giovanni Girolamo Saccheri.[30]

In the early 17th century, there were two important developments in geometry. The first was the creation of analytic geometry, or geometry with coordinates and equations, by René Descartes (1596–1650) and Pierre de Fermat (1601–1665). This was a necessary precursor to the development of calculus and a precise quantitative science of physics. The second geometric development of this period was the systematic study of projective geometry by Girard Desargues (1591–1661). Projective geometry is a geometry without measurement or parallel lines, just the study of how points are related to each other.

Two developments in geometry in the 19th century changed the way it had been studied previously. These were the discovery of non-Euclidean geometries by Nikolai Ivanovich Lobachevsky, János Bolyai and Carl Friedrich Gauss and of the formulation of symmetry as the central consideration in the Erlangen Programme of Felix Klein (which generalized the Euclidean and non-Euclidean geometries). Two of the master geometers of the time were Bernhard Riemann (1826–1866), working primarily with tools from mathematical analysis, and introducing the Riemann surface, and Henri Poincaré, the founder of algebraic topology and the geometric theory of dynamical systems. As a consequence of these major changes in the conception of geometry, the concept of "space" became something rich and varied, and the natural background for theories as different as complex analysis and classical mechanics.

Important concepts in geometry

The following are some of the most important concepts in geometry.[6][7]

Axioms

An illustration of Euclid's parallel postulate
See also: Euclidean geometry

Euclid took an abstract approach to geometry in his Elements, one of the most influential books ever written. Euclid introduced certain axioms, or postulates, expressing primary or self-evident properties of points, lines, and planes. He proceeded to rigorously deduce other properties by mathematical reasoning. The characteristic feature of Euclid's approach to geometry was its rigor, and it has come to be known as axiomatic or synthetic geometry. At the start of the 19th century, the discovery of non-Euclidean geometries by Nikolai Ivanovich Lobachevsky (1792–1856), János Bolyai (1802–1860), Carl Friedrich Gauss (1777–1855) and others led to a revival of interest in this discipline, and in the 20th century, David Hilbert (1862–1943) employed axiomatic reasoning in an attempt to provide a modern foundation of geometry.

Points

Main article: Point (geometry)

Points are considered fundamental objects in Euclidean geometry. They have been defined in a variety of ways, including Euclid's definition as 'that which has no part'[31] and through the use of algebra or nested sets.[32] In many areas of geometry, such as analytic geometry, differential geometry, and topology, all objects are considered to be built up from points. However, there has been some study of geometry without reference to points.[33]

Lines

Main article: Line (geometry)

Euclid described a line as "breadthless length" which "lies equally with respect to the points on itself".[31] In modern mathematics, given the multitude of geometries, the concept of a line is closely tied to the way the geometry is described. For instance, in analytic geometry, a line in the plane is often defined as the set of points whose coordinates satisfy a given linear equation,[34] but in a more abstract setting, such as incidence geometry, a line may be an independent object, distinct from the set of points which lie on it.[35] In differential geometry, a geodesic is a generalization of the notion of a line to curved spaces.[36]

Planes

Main article: Plane (geometry)

A plane is a flat, two-dimensional surface that extends infinitely far.[31] Planes are used in every area of geometry. For instance, planes can be studied as a topological surface without reference to distances or angles;[37] it can be studied as an affine space, where collinearity and ratios can be studied but not distances;[38] it can be studied as the complex plane using techniques of complex analysis;[39] and so on.

Angles

Main article: Angle

Euclid defines a plane angle as the inclination to each other, in a plane, of two lines which meet each other, and do not lie straight with respect to each other.[31] In modern terms, an angle is the figure formed by two rays, called the sides of the angle, sharing a common endpoint, called the vertex of the angle.[40]

Acute (a), obtuse (b), and straight (c) angles. The acute and obtuse angles are also known as oblique angles.

In Euclidean geometry, angles are used to study polygons and triangles, as well as forming an object of study in their own right.[31] The study of the angles of a triangle or of angles in a unit circle forms the basis of trigonometry.[41]

In differential geometry and calculus, the angles between plane curves or space curves or surfaces can be calculated using the derivative.[42][43]

Curves

Main article: Curve (geometry)

A curve is a 1-dimensional object that may be straight (like a line) or not; curves in 2-dimensional space are called plane curves and those in 3-dimensional space are called space curves.[44]

In topology, a curve is defined by a function from an interval of the real numbers to another space.[37] In differential geometry, the same definition is used, but the defining function is required to be differentiable [45] Algebraic geometry studies algebraic curves, which are defined as algebraic varieties of dimension one.[46]

Surfaces

Main article: Surface (mathematics)
A sphere is a surface that can be defined parametrically (by x = r sin θ cos φ, y = r sin θ sin φ, z = r cos θ) or implicitly (by x2 + y2 + z2 − r2 = 0.)

A surface is a two-dimensional object, such as a sphere or paraboloid.[47] In differential geometry[45] and topology,[37] surfaces are described by two-dimensional 'patches' (or neighborhoods) that are assembled by diffeomorphisms or homeomorphisms, respectively. In algebraic geometry, surfaces are described by polynomial equations.[46]

Manifolds

Main article: Manifold

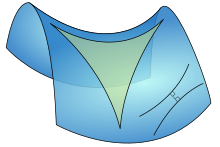
A manifold is a generalization of the concepts of curve and surface. In topology, a manifold is a topological space where every point has a neighborhood that is homeomorphic to Euclidean space.[37] In differential geometry, a differentiable manifold is a space where each neighborhood is diffeomorphic to Euclidean space.[45]

Manifolds are used extensively in physics, including in general relativity and string theory[48]

Topologies and metrics

Main article: Topology
Visual checking of the Pythagorean theorem for the (3, 4, 5) triangle as in the Zhoubi Suanjing 500–200 BC. The Pythagorean theorem is a consequence of the Euclidean metric.

A topology is a mathematical structure on a set that tells how elements of the set relate spatially to each other.[37] The best-known examples of topologies come from metrics, which are ways of measuring distances between points.[49] For instance, the Euclidean metric measures the distance between points in the Euclidean plane, while the hyperbolic metric measures the distance in the hyperbolic plane. Other important examples of metrics include the Lorentz metric of special relativity and the semi-Riemannian metrics of general relativity.[50]

Compass and straightedge constructions

Main article: Compass and straightedge constructions

Classical geometers paid special attention to constructing geometric objects that had been described in some other way. Classically, the only instruments allowed in geometric constructions are the compass and straightedge. Also, every construction had to be complete in a finite number of steps. However, some problems turned out to be difficult or impossible to solve by these means alone, and ingenious constructions using parabolas and other curves, as well as mechanical devices, were found.

Dimension

Main article: Dimension
The Koch snowflake, with fractal dimension=log4/log3 and topological dimension=1

Where the traditional geometry allowed dimensions 1 (a line), 2 (a plane) and 3 (our ambient world conceived of as three-dimensional space), mathematicians have used higher dimensions for nearly two centuries. The concept of dimension has gone through stages of being any natural number n, to being possibly infinite with the introduction of Hilbert space, to being any positive real number in fractal geometry. Dimension theory is a technical area, initially within general topology, that discusses definitions; in common with most mathematical ideas, dimension is now defined rather than an intuition. Connected topological manifolds have a well-defined dimension; this is a theorem (invariance of domain) rather than anything a priori.

The issue of dimension still matters to geometry as many classic questions still lack complete answers. For instance, many open problems in topology depend on the dimension of an object for the result. In physics, dimensions 3 of space and 4 of space-time are special cases in geometric topology, and dimensions 10 and 11 are key ideas in string theory. Currently, the existence of the theoretical dimensions is purely defined by technical reasons; it is likely that further research may result in a geometric reason for the significance of 10 or 11 dimensions in the theory, lending credibility or possibly disproving string theory.

Symmetry

Main article: Symmetry
A tiling of the hyperbolic plane

The theme of symmetry in geometry is nearly as old as the science of geometry itself. Symmetric shapes such as the circle, regular polygons and platonic solids held deep significance for many ancient philosophers and were investigated in detail before the time of Euclid. Symmetric patterns occur in nature and were artistically rendered in a multitude of forms, including the graphics of M.C. Escher. Nonetheless, it was not until the second half of 19th century that the unifying role of symmetry in foundations of geometry was recognized. Felix Klein's Erlangen program proclaimed that, in a very precise sense, symmetry, expressed via the notion of a transformation group, determines what geometry is. Symmetry in classical Euclidean geometry is represented by congruences and rigid motions, whereas in projective geometry an analogous role is played by collineations, geometric transformations that take straight lines into straight lines. However it was in the new geometries of Bolyai and Lobachevsky, Riemann, Clifford and Klein, and Sophus Lie that Klein's idea to 'define a geometry via its symmetry group' proved most influential. Both discrete and continuous symmetries play prominent roles in geometry, the former in topology and geometric group theory, the latter in Lie theory and Riemannian geometry.

A different type of symmetry is the principle of duality in projective geometry (see Duality (projective geometry)) among other fields. This meta-phenomenon can roughly be described as follows: in any theorem, exchange point with plane, join with meet, lies in with contains, and you will get an equally true theorem. A similar and closely related form of duality exists between a vector space and its dual space.

Non-Euclidean geometry

Differential geometry uses tools from calculus to study problems involving curvature.

In the nearly two thousand years since Euclid, while the range of geometrical questions asked and answered inevitably expanded, the basic understanding of space remained essentially the same. Immanuel Kant argued that there is only one, absolute, geometry, which is known to be true a priori by an inner faculty of mind: Euclidean geometry was synthetic a priori.[51] This dominant view was overturned by the revolutionary discovery of non-Euclidean geometry in the works of Bolyai, Lobachevsky, and Gauss (who never published his theory). They demonstrated that ordinary Euclidean space is only one possibility for development of geometry. A broad vision of the subject of geometry was then expressed by Riemann in his 1867 inauguration lecture Über die Hypothesen, welche der Geometrie zu Grunde liegen (On the hypotheses on which geometry is based),[52] published only after his death. Riemann's new idea of space proved crucial in Einstein's general relativity theory, and Riemannian geometry, that considers very general spaces in which the notion of length is defined, is a mainstay of modern geometry.

Contemporary geometry

Euclidean geometry

Geometry lessons in the 20th century

Euclidean geometry has become closely connected with computational geometry, computer graphics, convex geometry, incidence geometry, finite geometry, discrete geometry, and some areas of combinatorics. Attention was given to further work on Euclidean geometry and the Euclidean groups by crystallography and the work of H. S. M. Coxeter, and can be seen in theories of Coxeter groups and polytopes. Geometric group theory is an expanding area of the theory of more general discrete groups, drawing on geometric models and algebraic techniques.

Differential geometry

Differential geometry has been of increasing importance to mathematical physics due to Einstein's general relativity postulation that the universe is curved. Contemporary differential geometry is intrinsic, meaning that the spaces it considers are smooth manifolds whose geometric structure is governed by a Riemannian metric, which determines how distances are measured near each point, and not a priori parts of some ambient flat Euclidean space.

Topology and geometry

A thickening of the trefoil knot

The field of topology, which saw massive development in the 20th century, is in a technical sense a type of transformation geometry, in which transformations are homeomorphisms. This has often been expressed in the form of the dictum 'topology is rubber-sheet geometry'. Contemporary geometric topology and differential topology, and particular subfields such as Morse theory, would be counted by most mathematicians as part of geometry. Algebraic topology and general topology have gone their own ways.[citation needed][dubious – discuss]

Algebraic geometry

Quintic Calabi–Yau threefold

The field of algebraic geometry is the modern incarnation of the Cartesian geometry of co-ordinates. From late 1950s through mid-1970s it had undergone major foundational development, largely due to work of Jean-Pierre Serre and Alexander Grothendieck. This led to the introduction of schemes and greater emphasis on topological methods, including various cohomology theories. One of seven Millennium Prize problems, the Hodge conjecture, is a question in algebraic geometry.

The study of low-dimensional algebraic varieties, algebraic curves, algebraic surfaces and algebraic varieties of dimension 3 ("algebraic threefolds"), has been far advanced. Gröbner basis theory and real algebraic geometry are among more applied subfields of modern algebraic geometry. Arithmetic geometry is an active field combining algebraic geometry and number theory. Other directions of research involve moduli spaces and complex geometry. Algebro-geometric methods are commonly applied in string and brane theory.

Applications

Geometry has found applications in many fields, some of which are described below.

Art

Main article: Mathematics and art

Mathematics and art are related in a variety of ways. For instance, the theory of perspective showed that there is more to geometry than just the metric properties of figures: perspective is the origin of projective geometry.

Architecture

Main articles: Mathematics and architecture and Architectural geometry

Mathematics and architecture are related, since, as with other arts, architects use mathematics for several reasons. Apart from the mathematics needed when engineering buildings, architects use geometry: to define the spatial form of a building; from the Pythagoreans of the sixth century BC onwards, to create forms considered harmonious, and thus to lay out buildings and their surroundings according to mathematical, aesthetic and sometimes religious principles; to decorate buildings with mathematical objects such as tessellations; and to meet environmental goals, such as to minimise wind speeds around the bases of tall buildings.

Physics

Main article: Mathematical physics
The 421polytope, orthogonally projected into the E8 Lie group Coxeter plane. Lie groups have several applications in physics.

The field of astronomy, especially as it relates to mapping the positions of stars and planets on the celestial sphere and describing the relationship between movements of celestial bodies, have served as an important source of geometric problems throughout history.

Modern geometry has many ties to physics as is exemplified by the links between pseudo-Riemannian geometry and general relativity. One of the youngest physical theories, string theory, is also very geometric in flavour.

Other fields of mathematics

Geometry has also had a large effect on other areas of mathematics. For instance, the introduction of coordinates by René Descartes and the concurrent developments of algebra marked a new stage for geometry, since geometric figures such as plane curves could now be represented analytically in the form of functions and equations. This played a key role in the emergence of infinitesimal calculus in the 17th century. The subject of geometry was further enriched by the study of the intrinsic structure of geometric objects that originated with Euler and Gauss and led to the creation of topology and differential geometry.

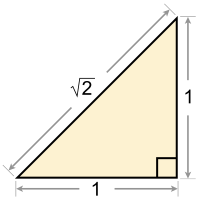
The Pythagoreans discovered that the sides of a triangle could have incommensurable lengths.

An important area of application is number theory. In ancient Greece the Pythagoreans considered the role of numbers in geometry. However, the discovery of incommensurable lengths, which contradicted their philosophical views, made them abandon abstract numbers in favor of concrete geometric quantities, such as length and area of figures. Since the 19th century, geometry has been used for solving problems in number theory, for example through the geometry of numbers or, more recently, scheme theory, which is used in Wiles's proof of Fermat's Last Theorem.

While the visual nature of geometry makes it initially more accessible than other mathematical areas such as algebra or number theory, geometric language is also used in contexts far removed from its traditional, Euclidean provenance (for example, in fractal geometry and algebraic geometry).[53]

Analytic geometry applies methods of algebra to geometric questions, typically by relating geometric curves to algebraic equations. These ideas played a key role in the development of calculus in the 17th century and led to the discovery of many new properties of plane curves. Modern algebraic geometry considers similar questions on a vastly more abstract level.

Leonhard Euler, in studying problems like the Seven Bridges of Königsberg, considered the most fundamental properties of geometric figures based solely on shape, independent of their metric properties. Euler called this new branch of geometry geometria situs (geometry of place), but it is now known as topology. Topology grew out of geometry, but turned into a large independent discipline. It does not differentiate between objects that can be continuously deformed into each other. The objects may nevertheless retain some geometry, as in the case of hyperbolic knots.

See also

Lists

Related topics

Other fields

Notes

  1. ^ a b (Boyer 1991, "Ionia and the Pythagoreans" p. 43)
  2. ^ Martin J. Turner,Jonathan M. Blackledge,Patrick R. Andrews (1998). Fractal geometry in digital imaging. Academic Press. p. 1. ISBN 0-12-703970-8
  3. ^ a b Staal, Frits (1999), "Greek and Vedic Geometry", Journal of Indian Philosophy, 27 (1–2): 105–127, doi:10.1023/A:1004364417713
  4. ^ a b O'Connor, John J.; Robertson, Edmund F., "Al-Sabi Thabit ibn Qurra al-Harrani", MacTutor History of Mathematics archive, University of St Andrews.
  5. ^ Lamb, Evelyn (2015-11-08). "By Solving the Mysteries of Shape-Shifting Spaces, Mathematician Wins $3-Million Prize". Scientific American. Retrieved 2016-08-29.
  6. ^ a b Tabak, John (2014). Geometry: the language of space and form. Infobase Publishing. p. xiv. ISBN 978-0816049530.
  7. ^ a b Schmidt, W., Houang, R., & Cogan, L. (2002). "A coherent curriculum". American Educator, 26(2), 1–18.
  8. ^ J. Friberg, "Methods and traditions of Babylonian mathematics. Plimpton 322, Pythagorean triples, and the Babylonian triangle parameter equations", Historia Mathematica, 8, 1981, pp. 277—318.
  9. ^ Neugebauer, Otto (1969) [1957]. The Exact Sciences in Antiquity (2 ed.). Dover Publications. ISBN 978-0-486-22332-2. Chap. IV "Egyptian Mathematics and Astronomy", pp. 71–96.
  10. ^ (Boyer 1991, "Egypt" p. 19)
  11. ^ Ossendrijver, Mathieu (29 Jan 2016). "Ancient Babylonian astronomers calculated Jupiter's position from the area under a time-velocity graph". Science. 351 (6272): 482–484. Bibcode:2016Sci...351..482O. doi:10.1126/science.aad8085. PMID 26823423. Retrieved 29 January 2016.
  12. ^ Depuydt, Leo (1 January 1998). "Gnomons at Meroë and Early Trigonometry". The Journal of Egyptian Archaeology. 84: 171–180. doi:10.2307/3822211. JSTOR 3822211.
  13. ^ Slayman, Andrew (May 27, 1998). "Neolithic Skywatchers". Archaeology Magazine Archive.
  14. ^ Eves, Howard, An Introduction to the History of Mathematics, Saunders, 1990, ISBN 0-03-029558-0.
  15. ^ Kurt Von Fritz (1945). "The Discovery of Incommensurability by Hippasus of Metapontum". The Annals of Mathematics.
  16. ^ James R. Choike (1980). "The Pentagram and the Discovery of an Irrational Number". The Two-Year College Mathematics Journal.
  17. ^ (Boyer 1991, "The Age of Plato and Aristotle" p. 92)
  18. ^ (Boyer 1991, "Euclid of Alexandria" p. 119)
  19. ^ (Boyer 1991, "Euclid of Alexandria" p. 104)
  20. ^ Howard Eves, An Introduction to the History of Mathematics, Saunders, 1990, ISBN 0-03-029558-0 p. 141: "No work, except The Bible, has been more widely used...."
  21. ^ O'Connor, J.J.; Robertson, E.F. (February 1996). "A history of calculus". University of St Andrews. Retrieved 2007-08-07.
  22. ^ Pythagorean triples are triples of integers with the property: . Thus, , , etc.
  23. ^ (Cooke 2005, p. 198): "The arithmetic content of the Śulva Sūtras consists of rules for finding Pythagorean triples such as (3, 4, 5), (5, 12, 13), (8, 15, 17), and (12, 35, 37). It is not certain what practical use these arithmetic rules had. The best conjecture is that they were part of religious ritual. A Hindu home was required to have three fires burning at three different altars. The three altars were to be of different shapes, but all three were to have the same area. These conditions led to certain "Diophantine" problems, a particular case of which is the generation of Pythagorean triples, so as to make one square integer equal to the sum of two others."
  24. ^ (Hayashi 2005, p. 371)
  25. ^ a b (Hayashi 2003, pp. 121–122)
  26. ^ R. Rashed (1994), The development of Arabic mathematics: between arithmetic and algebra, p. 35 London
  27. ^ Boyer (1991). "The Arabic Hegemony". A History of Mathematics. pp. 241–242. Omar Khayyam (c. 1050–1123), the "tent-maker," wrote an Algebra that went beyond that of al-Khwarizmi to include equations of third degree. Like his Arab predecessors, Omar Khayyam provided for quadratic equations both arithmetic and geometric solutions; for general cubic equations, he believed (mistakenly, as the 16th century later showed), arithmetic solutions were impossible; hence he gave only geometric solutions. The scheme of using intersecting conics to solve cubics had been used earlier by Menaechmus, Archimedes, and Alhazan, but Omar Khayyam took the praiseworthy step of generalizing the method to cover all third-degree equations (having positive roots). .. For equations of higher degree than three, Omar Khayyam evidently did not envision similar geometric methods, for space does not contain more than three dimensions, ... One of the most fruitful contributions of Arabic eclecticism was the tendency to close the gap between numerical and geometric algebra. The decisive step in this direction came much later with Descartes, but Omar Khayyam was moving in this direction when he wrote, "Whoever thinks algebra is a trick in obtaining unknowns has thought it in vain. No attention should be paid to the fact that algebra and geometry are different in appearance. Algebras are geometric facts which are proved."
  28. ^ O'Connor, John J.; Robertson, Edmund F., "Al-Mahani", MacTutor History of Mathematics archive, University of St Andrews.
  29. ^ O'Connor, John J.; Robertson, Edmund F., "Omar Khayyam", MacTutor History of Mathematics archive, University of St Andrews.
  30. ^ Boris A. Rosenfeld and Adolf P. Youschkevitch (1996), "Geometry", in Roshdi Rashed, ed., Encyclopedia of the History of Arabic Science, Vol. 2, pp. 447–494 [470], Routledge, London and New York:

    "Three scientists, Ibn al-Haytham, Khayyam, and al-Tusi, had made the most considerable contribution to this branch of geometry whose importance came to be completely recognized only in the 19th century. In essence, their propositions concerning the properties of quadrangles which they considered, assuming that some of the angles of these figures were acute of obtuse, embodied the first few theorems of the hyperbolic and the elliptic geometries. Their other proposals showed that various geometric statements were equivalent to the Euclidean postulate V. It is extremely important that these scholars established the mutual connection between this postulate and the sum of the angles of a triangle and a quadrangle. By their works on the theory of parallel lines Arab mathematicians directly influenced the relevant investigations of their European counterparts. The first European attempt to prove the postulate on parallel lines – made by Witelo, the Polish scientists of the 13th century, while revising Ibn al-Haytham's Book of Optics (Kitab al-Manazir) – was undoubtedly prompted by Arabic sources. The proofs put forward in the 14th century by the Jewish scholar Levi ben Gerson, who lived in southern France, and by the above-mentioned Alfonso from Spain directly border on Ibn al-Haytham's demonstration. Above, we have demonstrated that Pseudo-Tusi's Exposition of Euclid had stimulated both J. Wallis's and G. Saccheri's studies of the theory of parallel lines."

  31. ^ a b c d e Euclid's Elements – All thirteen books in one volume, Based on Heath's translation, Green Lion Press ISBN 1-888009-18-7.
  32. ^ Clark, Bowman L. (Jan 1985). "Individuals and Points". Notre Dame Journal of Formal Logic. 26 (1): 61–75. doi:10.1305/ndjfl/1093870761. Retrieved 29 August 2016.
  33. ^ Gerla, G., 1995, "Pointless Geometries" in Buekenhout, F., Kantor, W. eds., Handbook of incidence geometry: buildings and foundations. North-Holland: 1015–1031.
  34. ^ John Casey (1885) Analytic Geometry of the Point, Line, Circle, and Conic Sections, link from Internet Archive.
  35. ^ Buekenhout, Francis (1995), Handbook of Incidence Geometry: Buildings and Foundations, Elsevier B.V.
  36. ^ "geodesic – definition of geodesic in English from the Oxford dictionary". OxfordDictionaries.com. Retrieved 2016-01-20.
  37. ^ a b c d e Munkres, James R. Topology. Vol. 2. Upper Saddle River: Prentice Hall, 2000.
  38. ^ Szmielew, Wanda. 'From affine to Euclidean geometry: An axiomatic approach.' Springer, 1983.
  39. ^ Ahlfors, Lars V. Complex analysis: an introduction to the theory of analytic functions of one complex variable. New York, London (1953).
  40. ^ Sidorov, L.A. (2001) [1994], "Angle", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer Science+Business Media B.V. / Kluwer Academic Publishers, ISBN 978-1-55608-010-4
  41. ^ Gelʹfand, Izrailʹ Moiseevič, and Mark Saul. "Trigonometry." 'Trigonometry'. Birkhäuser Boston, 2001. 1–20.
  42. ^ Stewart, James (2012). Calculus: Early Transcendentals, 7th ed., Brooks Cole Cengage Learning. ISBN 978-0-538-49790-9
  43. ^ Jost, Jürgen (2002), Riemannian Geometry and Geometric Analysis, Berlin: Springer-Verlag, ISBN 978-3-540-42627-1.
  44. ^ Baker, Henry Frederick. Principles of geometry. Vol. 2. CUP Archive, 1954.
  45. ^ a b c Do Carmo, Manfredo Perdigao, and Manfredo Perdigao Do Carmo. Differential geometry of curves and surfaces. Vol. 2. Englewood Cliffs: Prentice-hall, 1976.
  46. ^ a b Mumford, David (1999). The Red Book of Varieties and Schemes Includes the Michigan Lectures on Curves and Their Jacobians (2nd ed.). Springer-Verlag. ISBN 978-3-540-63293-1. Zbl 0945.14001.
  47. ^ Briggs, William L., and Lyle Cochran Calculus. "Early Transcendentals." ISBN 978-0321570567.
  48. ^ Yau, Shing-Tung; Nadis, Steve (2010). The Shape of Inner Space: String Theory and the Geometry of the Universe's Hidden Dimensions. Basic Books. ISBN 978-0-465-02023-2.
  49. ^ Dmitri Burago, Yu D Burago, Sergei Ivanov, A Course in Metric Geometry, American Mathematical Society, 2001, ISBN 0-8218-2129-6.
  50. ^ Wald, Robert M. (1984), General Relativity, University of Chicago Press, ISBN 978-0-226-87033-5
  51. ^ Kline (1972) "Mathematical thought from ancient to modern times", Oxford University Press, p. 1032. Kant did not reject the logical (analytic a priori) possibility of non-Euclidean geometry, see Jeremy Gray, "Ideas of Space Euclidean, Non-Euclidean, and Relativistic", Oxford, 1989; p. 85. Some have implied that, in light of this, Kant had in fact predicted the development of non-Euclidean geometry, cf. Leonard Nelson, "Philosophy and Axiomatics," Socratic Method and Critical Philosophy, Dover, 1965, p. 164.
  52. ^ "Ueber die Hypothesen, welche der Geometrie zu Grunde liegen". Archived from the original on 18 March 2016.
  53. ^ It is quite common in algebraic geometry to speak about geometry of algebraic varieties over finite fields, possibly singular. From a naïve perspective, these objects are just finite sets of points, but by invoking powerful geometric imagery and using well developed geometric techniques, it is possible to find structure and establish properties that make them somewhat analogous to the ordinary spheres or cones.

Sources

  • Boyer, C.B. (1991) [1989]. A History of Mathematics (Second edition, revised by Uta C. Merzbach ed.). New York: Wiley. ISBN 978-0-471-54397-8.
  • Cooke, Roger (2005), The History of Mathematics:, New York: Wiley-Interscience, 632 pages, ISBN 978-0-471-44459-6
  • Hayashi, Takao (2003), "Indian Mathematics", in Grattan-Guinness, Ivor, Companion Encyclopedia of the History and Philosophy of the Mathematical Sciences, 1, Baltimore, MD: The Johns Hopkins University Press, 976 pages, pp. 118–130, ISBN 978-0-8018-7396-6
  • Hayashi, Takao (2005), "Indian Mathematics", in Flood, Gavin, The Blackwell Companion to Hinduism, Oxford: Basil Blackwell, 616 pages, pp. 360–375, ISBN 978-1-4051-3251-0
  • Nikolai I. Lobachevsky, Pangeometry, translator and editor: A. Papadopoulos, Heritage of European Mathematics Series, Vol. 4, European Mathematical Society, 2010.

Further reading

External links

Library resources about
Geometry

Retrieved from "https://en.wikipedia.org/w/index.php?title=Geometry&oldid=870369655"