Maximum likelihood estimation

This article is about the statistical techniques. For computer data storage, see Partial response maximum likelihood.

In statistics, maximum likelihood estimation (MLE) is a method of estimating the parameters of a statistical model, given observations. The method obtains the parameter estimates by finding the parameter values that maximize the likelihood function. The estimates are called maximum likelihood estimates, which is also abbreviated as MLE.

The method of maximum likelihood is used with a wide range of statistical analyses. As an example, suppose that we are interested in the heights of adult female penguins, but are unable to measure the height of every penguin in a population (due to cost or time constraints). Assuming that the heights are normally distributed with some unknown mean and variance, the mean and variance can be estimated with MLE while only knowing the heights of some sample of the overall population. MLE would accomplish that by taking the mean and variance as parameters and finding particular parametric values that make the observed results the most probable given the normal model.

From the point of view of Bayesian inference, MLE is a special case of maximum a posteriori estimation (MAP) that assumes a uniform prior distribution of the parameters. In frequentist inference, MLE is one of several methods to get estimates of parameters without using prior distributions. Priors are avoided by not making probability statements about the parameters, but only about their estimates, whose properties are fully defined by the observations and the statistical model.

Principles

The method of maximum likelihood is based on the likelihood function, ${\mathcal {L}}(\theta \,;x)$. We are given a statistical model, i.e. a family of distributions $\{f(\cdot \,;\theta )\mid \theta \in \Theta \}$, where $\theta$ denotes the (possibly multi-dimensional) parameter for the model. The method of maximum likelihood finds the values of the model parameter, $\theta$, that maximize the likelihood function, ${\mathcal {L}}(\theta \,;x)$. Intuitively, this selects the parameter values that make the data most probable.

The method defines a maximum likelihood estimate:

${\hat {\theta }}\in \{{\underset {\theta \in \Theta }{\operatorname {arg\,max} }}\ {\mathcal {L}}(\theta \,;x)\},$

if a maximum exists.

In practice, it is often convenient to work with the natural logarithm of the likelihood function, called the log-likelihood:

$\ell (\theta \,;x)=\ln {\mathcal {L}}(\theta \,;x),$

or the average log-likelihood:

${\hat {\ell }}(\theta \,;x)={\frac {1}{n}}\ln {\mathcal {L(\theta \,;x)}}.$

The hat over $\ell$ indicates that it is akin to an estimator. Indeed, ${\hat {\ell }}$ estimates the expected log-likelihood of a single observation in the model.

An MLE is the same regardless of whether we maximize the likelihood or the log-likelihood, because log is a strictly increasing function.

For many models, a maximum likelihood estimator can be found as an explicit function of the observed data $x$. For many other models, however, no closed-form solution to the maximization problem is known or available, and an MLE can only be found via numerical global optimization. For some problems, there may be multiple values that maximize the likelihood. For other problems, no maximum likelihood estimate exists: either the log-likelihood function increases without ever reaching a supremum value, or the supremum does exist but is outside the bounds of $\Theta$, the set of acceptable parameter values.

Properties

A maximum likelihood estimator is an extremum estimator obtained by maximizing, as a function of θ, the objective function (cf. loss function) ${\hat {\ell }}(\theta \,;x)$. If the data are independent and identically distributed, then we have

${\hat {\ell }}(\theta \,;x)={\frac {1}{n}}\sum _{i=1}^{n}\ln f(x_{i}\mid \theta ),$

this being the sample analogue of the expected log-likelihood $\ell (\theta )=\operatorname {E} [\,\ln f(x_{i}\mid \theta )\,]$, where this expectation is taken with respect to the true density.

Maximum-likelihood estimators have no optimum properties for finite samples, in the sense that (when evaluated on finite samples) other estimators may have greater concentration around the true parameter-value. However, like other estimation methods, maximum likelihood estimation possesses a number of attractive limiting properties: As the sample size increases to infinity, sequences of maximum likelihood estimators have these properties:

• Consistency: the sequence of MLEs converges in probability to the value being estimated.
• Efficiency, i.e. it achieves the Cramér–Rao lower bound when the sample size tends to infinity. This means that no consistent estimator has lower asymptotic mean squared error than the MLE (or other estimators attaining this bound).
• Second-order efficiency after correction for bias.

Consistency

Under the conditions outlined below, the maximum likelihood estimator is consistent. The consistency means that if the data were generated by $f(\cdot \,;\theta _{0})$ and we have a sufficiently large number of observations n, then it is possible to find the value of θ₀ with arbitrary precision. In mathematical terms this means that as n goes to infinity the estimator ${\hat {\theta }}$ converges in probability to its true value:

${\hat {\theta }}_{\mathrm {mle} }\ {\xrightarrow {\text{p}}}\ \theta _{0}.$

Under slightly stronger conditions, the estimator converges almost surely (or strongly):

${\hat {\theta }}_{\mathrm {mle} }\ {\xrightarrow {\text{a.s.}}}\ \theta _{0}.$

Note that, in practical applications, data is never generated by $f(\cdot \,;\theta _{0})$. Rather, $f(\cdot \,;\theta _{0})$ is a model, often in idealized form, of the process that generated the data. It is a common aphorism in statistics that all models are wrong. Thus, true consistency does not occur in practical applications. Nevertheless, consistency is often considered to be a desirable property for an estimator to have.

To establish consistency, the following conditions are sufficient.

1. Identification of the model:

   $\theta \neq \theta _{0}\quad \Leftrightarrow \quad f(\cdot \mid \theta )\neq f(\cdot \mid \theta _{0}).$

   In other words, different parameter values θ correspond to different distributions within the model. If this condition did not hold, there would be some value θ₁ such that θ₀ and θ₁ generate an identical distribution of the observable data. Then we would not be able to distinguish between these two parameters even with an infinite amount of data—these parameters would have been observationally equivalent.
   

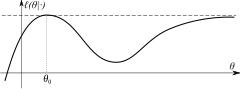
   The identification condition is absolutely necessary for the ML estimator to be consistent. When this condition holds, the limiting likelihood function ℓ(θ|·) has unique global maximum at θ₀.
2. Compactness: the parameter space Θ of the model is compact.
   

   The identification condition establishes that the log-likelihood has a unique global maximum. Compactness implies that the likelihood cannot approach the maximum value arbitrarily close at some other point (as demonstrated for example in the picture on the right).

   Compactness is only a sufficient condition and not a necessary condition. Compactness can be replaced by some other conditions, such as:

   • both concavity of the log-likelihood function and compactness of some (nonempty) upper level sets of the log-likelihood function, or
   • existence of a compact neighborhood N of θ₀ such that outside of N the log-likelihood function is less than the maximum by at least some ε > 0.
3. Continuity: the function ln f(x|θ) is continuous in θ for almost all values of x:

   $\operatorname {P} \!{\big [}\;\ln f(x\mid \theta )\;\in \;\mathbb {C} ^{0}(\Theta )\;{\big ]}=1.$

   The continuity here can be replaced with a slightly weaker condition of upper semi-continuity.
4. Dominance: there exists D(x) integrable with respect to the distribution f(x|θ₀) such that

   ${\big |}\ln f(x\mid \theta ){\big |}<D(x)\quad {\text{ for all }}\theta \in \Theta .$

   By the uniform law of large numbers, the dominance condition together with continuity establish the uniform convergence in probability of the log-likelihood:

   $\sup _{\theta \in \Theta }{\big |}{\hat {\ell }}(\theta \mid x)-\ell (\theta )\,{\big |}\ {\xrightarrow {\text{p}}}\ 0.$

The dominance condition can be employed in the case of i.i.d. observations. In the non-i.i.d. case, the uniform convergence in probability can be checked by showing that the sequence ${\hat {\ell }}(\theta \mid x)$ is stochastically equicontinuous. If one wants to demonstrate that the ML estimator ${\hat {\theta }}$ converges to θ₀ almost surely, then a stronger condition of uniform convergence almost surely has to be imposed:

$\sup _{\theta \in \Theta }{\big \|}\;{\hat {\ell }}(x\mid \theta )-\ell (\theta )\;{\big \|}\ {\xrightarrow {\text{a.s.}}}\ 0.$

Additionally, if (as assumed above) the data were generated by $f(\cdot \,;\theta _{0})$, then under certain conditions, it can also be shown that the maximum likelihood estimator converges in distribution to a normal distribution. Specifically,

${\sqrt {n}}{\big (}{\hat {\theta }}_{\mathrm {mle} }-\theta _{0}{\big )}\ {\xrightarrow {d}}\ {\mathcal {N}}(0,\,I^{-1})$

where I is the Fisher information matrix.

Functional invariance

The maximum likelihood estimator selects the parameter value which gives the observed data the largest possible probability (or probability density, in the continuous case). If the parameter consists of a number of components, then we define their separate maximum likelihood estimators, as the corresponding component of the MLE of the complete parameter. Consistent with this, if ${\widehat {\theta }}$ is the MLE for $\theta$, and if $g(\theta )$ is any transformation of $\theta$, then the MLE for $\alpha =g(\theta )$ is by definition

${\widehat {\alpha }}=g(\,{\widehat {\theta }}\,).\,$

It maximizes the so-called profile likelihood:

${\bar {L}}(\alpha )=\sup _{\theta :\alpha =g(\theta )}L(\theta ).\,$

The MLE is also invariant with respect to certain transformations of the data. If $y=g(x)$ where $g$ is one to one and does not depend on the parameters to be estimated, then the density functions satisfy

$f_{Y}(y)={\frac {f_{X}(x)}{|g'(x)|}}$

and hence the likelihood functions for $X$ and $Y$ differ only by a factor that does not depend on the model parameters.

For example, the MLE parameters of the log-normal distribution are the same as those of the normal distribution fitted to the logarithm of the data.

Higher-order properties

As noted above, the maximum likelihood estimator is √n -consistent and asymptotically efficient, meaning that it reaches the Cramér–Rao bound:

${\sqrt {n}}({\hat {\theta }}_{\text{mle}}-\theta _{0})\ \ {\xrightarrow {d}}\ \ {\mathcal {N}}(0,\ I^{-1}),$

where $I$ is the Fisher information matrix:

$I_{jk}=\operatorname {E} _{X}{\bigg [}\;{-{\frac {\partial ^{2}\ln f_{\theta _{0}}(X_{t})}{\partial \theta _{j}\,\partial \theta _{k}}}}\;{\bigg ]}.$

In particular, it means that the bias of the maximum likelihood estimator is equal to zero up to the order ​¹⁄_√n . However, when we consider the higher-order terms in the expansion of the distribution of this estimator, it turns out that θ_mle has bias of order ​¹⁄_n. This bias is equal to (componentwise)

$b_{h}\equiv \operatorname {E} {\bigg [}\;({\hat {\theta }}_{\mathrm {mle} }-\theta _{0})_{h}\;{\bigg ]}={\frac {1}{n}}\sum _{i,j,k=1}^{n}I^{hi}I^{jk}{\big (}{\frac {1}{2}}K_{ijk}+J_{j,ik}{\big )}$

where $I^{jk}$ denotes the (j,k)-th component of the inverse Fisher information matrix $I^{-1}$, and

${\tfrac {1}{2}}K_{ijk}+J_{j,ik}=\operatorname {E} _{X}{\bigg [}\;{\frac {1}{2}}{\frac {\partial ^{3}\ln f_{\theta _{0}}(X_{t})}{\partial \theta _{i}\,\partial \theta _{j}\,\partial \theta _{k}}}+{\frac {\partial \ln f_{\theta _{0}}(X_{t})}{\partial \theta _{j}}}{\frac {\partial ^{2}\ln f_{\theta _{0}}(X_{t})}{\partial \theta _{i}\,\partial \theta _{k}}}\;{\bigg ]}.$

Using these formulae it is possible to estimate the second-order bias of the maximum likelihood estimator, and correct for that bias by subtracting it:

${\hat {\theta }}_{\text{mle}}^{*}={\hat {\theta }}_{\text{mle}}-{\hat {b}}.$

This estimator is unbiased up to the terms of order ​¹⁄_n, and is called the bias-corrected maximum likelihood estimator.

This bias-corrected estimator is second-order efficient (at least within the curved exponential family), meaning that it has minimal mean squared error among all second-order bias-corrected estimators, up to the terms of the order ​¹⁄_n ². It is possible to continue this process, that is to derive the third-order bias-correction term, and so on. However, as was shown by Kano (1996), the maximum likelihood estimator is not third-order efficient.

Relation to Bayesian inference

A maximum likelihood estimator coincides with the most probable Bayesian estimator given a uniform prior distribution on the parameters. Indeed, the maximum a posteriori estimate is the parameter θ that maximizes the probability of θ given the data, given by Bayes' theorem:

$\operatorname {P} (\theta \mid x_{1},x_{2},\ldots ,x_{n})={\frac {f(x_{1},x_{2},\ldots ,x_{n}\mid \theta )\operatorname {P} (\theta )}{\operatorname {P} (x_{1},x_{2},\ldots ,x_{n})}}$

where $P(\theta )$ is the prior distribution for the parameter θ and where $\operatorname {P} (x_{1},x_{2},\ldots ,x_{n})$ is the probability of the data averaged over all parameters. Since the denominator is independent of θ, the Bayesian estimator is obtained by maximizing $f(x_{1},x_{2},\ldots ,x_{n}\mid \theta )\operatorname {P} (\theta )$ with respect to θ. If we further assume that the prior $P(\theta )$ is a uniform distribution, the Bayesian estimator is obtained by maximizing the likelihood function $f(x_{1},x_{2},\ldots ,x_{n}\mid \theta )$. Thus the Bayesian estimator coincides with the maximum likelihood estimator for a uniform prior distribution $\operatorname {P} (\theta )$.

Examples

Discrete uniform distribution

Main article: German tank problem

Consider a case where n tickets numbered from 1 to n are placed in a box and one is selected at random (see uniform distribution); thus, the sample size is 1. If n is unknown, then the maximum likelihood estimator ${\hat {n}}$ of n is the number m on the drawn ticket. (The likelihood is 0 for n < m, ​¹⁄_n for n ≥ m, and this is greatest when n = m. Note that the maximum likelihood estimate of n occurs at the lower extreme of possible values {m, m + 1, ...}, rather than somewhere in the "middle" of the range of possible values, which would result in less bias.) The expected value of the number m on the drawn ticket, and therefore the expected value of ${\hat {n}}$, is (n + 1)/2. As a result, with a sample size of 1, the maximum likelihood estimator for n will systematically underestimate n by (n − 1)/2.

Discrete distribution, finite parameter space

Suppose one wishes to determine just how biased an unfair coin is. Call the probability of tossing a ‘head’ p. The goal then becomes to determine p.

Suppose the coin is tossed 80 times: i.e. the sample might be something like x₁ = H, x₂ = T, ..., x₈₀ = T, and the count of the number of heads "H" is observed.

The probability of tossing tails is 1 − p (so here p is θ above). Suppose the outcome is 49 heads and 31 tails, and suppose the coin was taken from a box containing three coins: one which gives heads with probability p = ​¹⁄₃, one which gives heads with probability p = ​¹⁄₂ and another which gives heads with probability p = ​²⁄₃. The coins have lost their labels, so which one it was is unknown. Using maximum likelihood estimation the coin that has the largest likelihood can be found, given the data that were observed. By using the probability mass function of the binomial distribution with sample size equal to 80, number successes equal to 49 but for different values of p (the "probability of success"), the likelihood function (defined below) takes one of three values:

${\begin{aligned}\operatorname {P} {\big [}\;\mathrm {H} =49\mid p={\tfrac {1}{3}}\;{\big ]}&={\binom {80}{49}}({\tfrac {1}{3}})^{49}(1-{\tfrac {1}{3}})^{31}\approx 0.000,\\[6pt]\operatorname {P} {\big [}\;\mathrm {H} =49\mid p={\tfrac {1}{2}}\;{\big ]}&={\binom {80}{49}}({\tfrac {1}{2}})^{49}(1-{\tfrac {1}{2}})^{31}\approx 0.012,\\[6pt]\operatorname {P} {\big [}\;\mathrm {H} =49\mid p={\tfrac {2}{3}}\;{\big ]}&={\binom {80}{49}}({\tfrac {2}{3}})^{49}(1-{\tfrac {2}{3}})^{31}\approx 0.054.\end{aligned}}$

The likelihood is maximized when p = ​²⁄₃, and so this is the maximum likelihood estimate for p.

Discrete distribution, continuous parameter space

Now suppose that there was only one coin but its p could have been any value 0 ≤ p ≤ 1. The likelihood function to be maximised is

$L(p)=f_{D}(\mathrm {H} =49\mid p)={\binom {80}{49}}p^{49}(1-p)^{31},$

and the maximisation is over all possible values 0 ≤ p ≤ 1.

likelihood function for proportion value of a binomial process (n = 10)

One way to maximize this function is by differentiating with respect to p and setting to zero:

${\begin{aligned}{0}&{}={\frac {\partial }{\partial p}}\left({\binom {80}{49}}p^{49}(1-p)^{31}\right),\\[8pt]{0}&{}=49p^{48}(1-p)^{31}-31p^{49}(1-p)^{30}\\[8pt]&{}=p^{48}(1-p)^{30}\left[49(1-p)-31p\right]\\[8pt]&{}=p^{48}(1-p)^{30}\left[49-80p\right]\end{aligned}}$

which has solutions p = 0, p = 1, and p = ​⁴⁹⁄₈₀. The solution which maximizes the likelihood is clearly p = ​⁴⁹⁄₈₀ (since p = 0 and p = 1 result in a likelihood of zero). Thus the maximum likelihood estimator for p is ​⁴⁹⁄₈₀.

This result is easily generalized by substituting a letter such as s in the place of 49 to represent the observed number of 'successes' of our Bernoulli trials, and a letter such as n in the place of 80 to represent the number of Bernoulli trials. Exactly the same calculation yields ​^s⁄_n which is the maximum likelihood estimator for any sequence of n Bernoulli trials resulting in s 'successes'.

Continuous distribution, continuous parameter space

For the normal distribution ${\mathcal {N}}(\mu ,\sigma ^{2})$ which has probability density function

$f(x\mid \mu ,\sigma ^{2})={\frac {1}{{\sqrt {2\pi \sigma ^{2}}}\ }}\exp {\left(-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}\right)},$

the corresponding probability density function for a sample of n independent identically distributed normal random variables (the likelihood) is

$f(x_{1},\ldots ,x_{n}\mid \mu ,\sigma ^{2})=\prod _{i=1}^{n}f(x_{i}\mid \mu ,\sigma ^{2})=\left({\frac {1}{2\pi \sigma ^{2}}}\right)^{n/2}\exp \left(-{\frac {\sum _{i=1}^{n}(x_{i}-\mu )^{2}}{2\sigma ^{2}}}\right),$

or more conveniently,

$f(x_{1},\ldots ,x_{n}\mid \mu ,\sigma ^{2})=\left({\frac {1}{2\pi \sigma ^{2}}}\right)^{n/2}\exp \left(-{\frac {\sum _{i=1}^{n}(x_{i}-{\bar {x}})^{2}+n({\bar {x}}-\mu )^{2}}{2\sigma ^{2}}}\right),$

where ${\bar {x}}$ is the sample mean.

This family of distributions has two parameters: θ = (μ, σ); so we maximize the likelihood, ${\mathcal {L}}(\mu ,\sigma )=f(x_{1},\ldots ,x_{n}\mid \mu ,\sigma )$, over both parameters simultaneously, or if possible, individually.

Since the logarithm function itself is a continuous strictly increasing function over the range of the likelihood, the values which maximize the likelihood will also maximize its logarithm (the log-likelihood itself is not necessarily strictly increasing). The log-likelihood can be written as follows:

$\log {\Big (}{\mathcal {L}}(\mu ,\sigma ){\Big )}=-{\frac {\,n\,}{2}}\log(2\pi \sigma ^{2})-{\frac {1}{2\sigma ^{2}}}\sum _{i=1}^{n}(\,x_{i}-\mu \,)^{2}$

(Note: the log-likelihood is closely related to information entropy and Fisher information.)

We now compute the derivatives of this log-likelihood as follows.

${\begin{aligned}0&={\frac {\partial }{\partial \mu }}\log {\Big (}{\mathcal {L}}(\mu ,\sigma ){\Big )}=0-{\frac {\;-2\!n({\bar {x}}-\mu )\;}{2\sigma ^{2}}}.\end{aligned}}$

This is solved by

${\hat {\mu }}={\bar {x}}=\sum _{i=1}^{n}{\frac {\,x_{i}\,}{n}}.$

This is indeed the maximum of the function, since it is the only turning point in μ and the second derivative is strictly less than zero. Its expected value is equal to the parameter μ of the given distribution,

$\operatorname {E} {\big [}\;{\widehat {\mu }}\;{\big ]}=\mu ,\,$

which means that the maximum likelihood estimator ${\widehat {\mu }}$ is unbiased.

Similarly we differentiate the log-likelihood with respect to σ and equate to zero:

${\begin{aligned}0&={\frac {\partial }{\partial \sigma }}\log {\Bigg [}\left({\frac {1}{2\pi \sigma ^{2}}}\right)^{n/2}\exp \left(-{\frac {\sum _{i=1}^{n}(x_{i}-{\bar {x}})^{2}+n({\bar {x}}-\mu )^{2}}{2\sigma ^{2}}}\right){\Bigg ]}\\[6pt]&={\frac {\partial }{\partial \sigma }}\left[{\frac {n}{2}}\log \left({\frac {1}{2\pi \sigma ^{2}}}\right)-{\frac {\sum _{i=1}^{n}(x_{i}-{\bar {x}})^{2}+n({\bar {x}}-\mu )^{2}}{2\sigma ^{2}}}\right]\\[6pt]&=-{\frac {\,n\,}{\sigma }}+{\frac {\sum _{i=1}^{n}(x_{i}-{\bar {x}})^{2}+n({\bar {x}}-\mu )^{2}}{\sigma ^{3}}}\end{aligned}}$

which is solved by

${\widehat {\sigma }}^{2}={\frac {1}{n}}\sum _{i=1}^{n}(x_{i}-\mu )^{2}.$

Inserting the estimate $\mu ={\widehat {\mu }}$ we obtain

${\widehat {\sigma }}^{2}={\frac {1}{n}}\sum _{i=1}^{n}(x_{i}-{\bar {x}})^{2}={\frac {1}{n}}\sum _{i=1}^{n}x_{i}^{2}-{\frac {1}{n^{2}}}\sum _{i=1}^{n}\sum _{j=1}^{n}x_{i}x_{j}.$

To calculate its expected value, it is convenient to rewrite the expression in terms of zero-mean random variables (statistical error) $\delta _{i}\equiv \mu -x_{i}$. Expressing the estimate in these variables yields

${\widehat {\sigma }}^{2}={\frac {1}{n}}\sum _{i=1}^{n}(\mu -\delta _{i})^{2}-{\frac {1}{n^{2}}}\sum _{i=1}^{n}\sum _{j=1}^{n}(\mu -\delta _{i})(\mu -\delta _{j}).$

Simplifying the expression above, utilizing the facts that $\operatorname {E} {\big [}\;\delta _{i}\;{\big ]}=0$ and $\operatorname {E} {\big [}\;\delta _{i}^{2}\;{\big ]}=\sigma ^{2}$, allows us to obtain

$\operatorname {E} {\big [}\;{\widehat {\sigma }}^{2}\;{\big ]}={\frac {\,n-1\,}{n}}\sigma ^{2}.$

This means that the estimator ${\widehat {\sigma }}$ is biased. However, ${\widehat {\sigma }}$ is consistent.

Formally we say that the maximum likelihood estimator for $\theta =(\mu ,\sigma ^{2})$ is

${\widehat {\theta }}=\left({\widehat {\mu }},{\widehat {\sigma }}^{2}\right).$

In this case the MLEs could be obtained individually. In general this may not be the case, and the MLEs would have to be obtained simultaneously.

The normal log-likelihood at its maximum takes a particularly simple form:

$\log {\Big (}{\mathcal {L}}({\hat {\mu }},{\hat {\sigma }}){\Big )}={\frac {\,-n\;\;}{2}}{\big (}\,\log(2\pi {\hat {\sigma }}^{2})+1\,{\big )}$

This maximum log-likelihood can be shown to be the same for more general least squares, even for non-linear least squares. This is often used in determining likelihood-based approximate confidence intervals and confidence regions, which are generally more accurate than those using the asymptotic normality discussed above.

Non-independent variables

It may be the case that variables are correlated, that is, not independent. Two random variables X and Y are independent only if their joint probability density function is the product of the individual probability density functions, i.e.

$f(x,y)=f(x)f(y)\,$

Suppose one constructs an order-n Gaussian vector out of random variables $(x_{1},\ldots ,x_{n})$, where each variable has means given by $(\mu _{1},\ldots ,\mu _{n})$. Furthermore, let the covariance matrix be denoted by ${\mathit {\Sigma }}$.

The joint probability density function of these n random variables is then given by:

$f(x_{1},\ldots ,x_{n})={\frac {1}{(2\pi )^{n/2}{\sqrt {{\text{det}}({\mathit {\Sigma }})}}}}\exp \left(-{\frac {1}{2}}\left[x_{1}-\mu _{1},\ldots ,x_{n}-\mu _{n}\right]{\mathit {\Sigma }}^{-1}\left[x_{1}-\mu _{1},\ldots ,x_{n}-\mu _{n}\right]^{\mathrm {T} }\right)$

In the two variable case, the joint probability density function is given by:

$f(x,y)={\frac {1}{2\pi \sigma _{x}\sigma _{y}{\sqrt {1-\rho ^{2}}}}}\exp \left[-{\frac {1}{2(1-\rho ^{2})}}\left({\frac {(x-\mu _{x})^{2}}{\sigma _{x}^{2}}}-{\frac {2\rho (x-\mu _{x})(y-\mu _{y})}{\sigma _{x}\sigma _{y}}}+{\frac {(y-\mu _{y})^{2}}{\sigma _{y}^{2}}}\right)\right]$

In this and other cases where a joint density function exists, the likelihood function is defined as above, in the section Principles, using this density.

Iterative procedures

Consider problems where both states $x_{i}$ and parameters such as $\sigma ^{2}$ require to be estimated. Iterative procedures such as Expectation-maximization algorithms may be used to solve joint state-parameter estimation problems.

For example, suppose that n samples of state estimates ${\hat {x}}_{i}$ together with a sample mean ${\bar {x}}$ have been calculated by either a minimum-variance Kalman filter or a minimum-variance smoother using a previous variance estimate ${\widehat {\sigma }}^{2}$. Then the next variance iterate may be obtained from the maximum likelihood estimate calculation

${\widehat {\sigma }}^{2}={\frac {1}{n}}\sum _{i=1}^{n}({\hat {x}}_{i}-{\bar {x}})^{2}.$

The convergence of MLEs within filtering and smoothing EM algorithms has been studied in the literature.

History

Early users of maximum likelihood were Carl Friedrich Gauss, Pierre-Simon Laplace, Thorvald N. Thiele, and Francis Ysidro Edgeworth.

Ronald Fisher in 1913

However its widespread use arose between 1912 and 1922 when Ronald Fisher recommended, widely popularized, and carefully analyzed maximum-likelihood estimation (with fruitless attempts at proofs).

Maximum-likelihood estimation finally transcended heuristic justification in a proof published by Samuel S. Wilks in 1938, now called Wilks' theorem. The theorem shows that the error in the logarithm of likelihood values for estimates from multiple independent samples is asymptotically χ ² distributed, which enables convenient determination of a confidence region around any one estimate of the parameters. The only difficult part of Wilks’ proof depends on the expected value of the Fisher information matrix, which ironically is provided by a theorem proven by Fisher. Wilks continued to improve on the generality of the theorem throughout his life, with his most general proof published in 1962.

Some of the theory behind maximum likelihood estimation was developed for Bayesian statistics.

Reviews of the development of maximum likelihood estimation have been provided by a number of authors.

See also

• Other estimation methods
  • Generalized method of moments are methods related to the likelihood equation in maximum likelihood estimation
  • M-estimator, an approach used in robust statistics
  • Maximum a posteriori (MAP) estimator, for a contrast in the way to calculate estimators when prior knowledge is postulated
  • Maximum spacing estimation, a related method that is more robust in many situations
  • Maximum entropy estimation
  • Method of moments (statistics), another popular method for finding parameters of distributions
  • Method of support, a variation of the maximum likelihood technique
  • Minimum distance estimation
  • Partial likelihood methods for panel data
  • Quasi-maximum likelihood estimator, an MLE estimator that is misspecified, but still consistent
  • Restricted maximum likelihood, a variation using a likelihood function calculated from a transformed set of data
• Related concepts:
  • Akaike information criterion, a criterion to compare statistical models, based on MLE
  • Extremum estimator, a more general class of estimators to which MLE belongs
  • Fisher information, information matrix, its relationship to covariance matrix of ML estimates
  • Mean squared error, a measure of how 'good' an estimator of a distributional parameter is (be it the maximum likelihood estimator or some other estimator)
  • RANSAC, a method to estimate parameters of a mathematical model given data that contains outliers
  • Rao–Blackwell theorem, which yields a process for finding the best possible unbiased estimator (in the sense of having minimal mean squared error); the MLE is often a good starting place for the process
  • Wilks’ Theorem provides a means of estimating the size and shape of the region of roughly equally-probable estimates for the population's parameter values, using the information from a single sample, using a chi-squared distribution

References: non-historical

• Cox, David R.; Snell, E. Joyce (1968). "A general definition of residuals". Journal of the Royal Statistical Society, Series B. 30: 248–275. JSTOR 2984505.
• Kano, Yutaka (1996). "Third-order efficiency implies fourth-order efficiency". Journal of the Japan Statistical Society. 26: 101–117. doi:10.14490/jjss1995.26.101.
• Newey, Whitney K.; McFadden, Daniel (1994). "Chapter 35: Large sample estimation and hypothesis testing". In Engle, Robert; McFadden, Dan. Handbook of Econometrics, Vol.4. Elsevier Science. pp. 2111–2245. ISBN 0-444-88766-0.

References: historical

• Aldrich, John (1997). "R. A. Fisher and the making of maximum likelihood 1912–1922". Statistical Science. 12 (3): 162–176. doi:10.1214/ss/1030037906. MR 1617519.
• Edgeworth, Francis Y. (Sep 1908). "On the probable errors of frequency-constants". Journal of the Royal Statistical Society. 71 (3): 499–512. doi:10.2307/2339293. JSTOR 2339293.
• Edgeworth, Francis Y. (Dec 1908). "On the probable errors of frequency-constants". Journal of the Royal Statistical Society. 71 (4): 651–678. doi:10.2307/2339378. JSTOR 2339378.
• Hald, Anders (1998). A history of mathematical statistics from 1750 to 1930. New York, NY: Wiley. ISBN 0-471-17912-4.
• Hald, Anders (1999). "On the history of maximum likelihood in relation to inverse probability and least squares". Statistical Science. 14 (2): 214–222. doi:10.1214/ss/1009212248. JSTOR 2676741.
• Pratt, John W. (1976). "F. Y. Edgeworth and R. A. Fisher on the efficiency of maximum likelihood estimation". The Annals of Statistics. 4 (3): 501–514. doi:10.1214/aos/1176343457. JSTOR 2958222.
• Savage, Leonard J. (1976). "On rereading R. A. Fisher". The Annals of Statistics. 4 (3): 441–500. doi:10.1214/aos/1176343456. JSTOR 2958221.
• Stigler, Stephen M. (1978). "Francis Ysidro Edgeworth, statistician". Journal of the Royal Statistical Society, Series A. 141 (3): 287–322. doi:10.2307/2344804. JSTOR 2344804.
• Stigler, Stephen M. (1986). The history of statistics: the measurement of uncertainty before 1900. Harvard University Press. ISBN 0-674-40340-1.
• Stigler, Stephen M. (1999). Statistics on the table: the history of statistical concepts and methods. Harvard University Press. ISBN 0-674-83601-4.
• Wilks, S. S. (1938), "The Large-Sample Distribution of the Likelihood Ratio for Testing Composite Hypotheses", Annals of Mathematical Statistics, 9: 60–62, doi:10.1214/aoms/1177732360.

Further reading

• Andersen, Erling B. (1970); "Asymptotic Properties of Conditional Maximum Likelihood Estimators", Journal of the Royal Statistical Society B 32, 283–301
• Andersen, Erling B. (1980); Discrete Statistical Models with Social Science Applications, North Holland, 1980
• Basu, Debabrata (1988); Statistical Information and Likelihood : A Collection of Critical Essays by Dr. D. Basu; in Ghosh, Jayanta K., editor; Lecture Notes in Statistics, Volume 45, Springer-Verlag, 1988
• Einicke, G.A. (2012). Smoothing, Filtering and Prediction: Estimating the Past, Present and Future. Rijeka, Croatia: Intech. ISBN 978-953-307-752-9.
• Ferguson, Thomas S. (1982). "An inconsistent maximum likelihood estimate". Journal of the American Statistical Association. 77 (380): 831–834. doi:10.1080/01621459.1982.10477894. JSTOR 2287314.
• Ferguson, Thomas S. (1996). A Course in Large Sample Theory. Chapman & Hall. ISBN 0-412-04371-8.
• Le Cam, Lucien (1990). "Maximum likelihood — an introduction". ISI Review. 58 (2): 153–171. doi:10.2307/1403464.
• Le Cam, Lucien; Yang, Grace Lo (2000). Asymptotics in Statistics: some basic concepts (Second ed.). Springer. ISBN 0-387-95036-2.
• Lehmann, Erich L.; Casella, George (1998). Theory of Point Estimation, 2nd ed. Springer. ISBN 0-387-98502-6.
• Millar, R. B. (2011). Maximum Likelihood Estimation and Inference. Wiley.
• Ruppert, David (2010). Statistics and Data Analysis for Financial Engineering. Springer. p. 98. ISBN 978-1-4419-7786-1.
• van der Vaart, Aad W. (1998). Asymptotic Statistics. ISBN 0-521-78450-6.

External links

• Hazewinkel, Michiel, ed. (2001) [1994], "Maximum-likelihood method", Encyclopedia of Mathematics, Springer Science+Business Media B.V. / Kluwer Academic Publishers, ISBN 978-1-55608-010-4
• Maximum Likelihood Estimation Primer (an excellent tutorial)
• Implementing MLE for your own likelihood function using R
• Myung, I. J. (2003). "Tutorial on maximum likelihood estimation". Journal of Mathematical Psychology. CiteSeerX 10.1.1.74.671.