Von Mangoldt-függvény

A matematikában a von Mangoldt-függvény egy Hans von Mangoldtról elnevezett számelméleti függvény. Példa arra, hogy egy fontos számelméleti függvény nem szükségképpen multiplikatív vagy additív.

Definíció

A Λ(n)-nel jelölt von Mangoldt-függvény definíciója:

$\Lambda (n)={\begin{cases}\log p&{\text{ha }}n=p^{k}{\text{ egy }}p{\text{ prímre és egy }}k\geq 1{\text{ egészre }},\\0&{\text{egyébként.}}\end{cases}}$

Λ(n) értékei az első kilenc pozitív egészre

$0,\log 2,\log 3,\log 2,\log 5,0,\log 7,\log 2,\log 3,$

ami az (A014963 sorozat az OEIS-ben) sorozathoz kapcsolódik.

Összegfüggvénye a ψ(x) Csebisev-függvény, aminek definíciója:

$\psi (x)=\sum _{n\leq x}\Lambda (n).$

A ψ(x) függvényre von Mangoldt explicit képletet is meghatározott, amiben a Riemann-féle zéta-függvény nem triviális gyökeinek összege is szerepel. EZ a prímszámtétel első bizonyításának fontos része volt.

Tulajdonságok

A von Mangoldt-függvény megfelel a következő azonosságnak:

$\log(n)=\sum _{d\mid n}\Lambda (d).$

Az összeg befutja azokat a pozitív egész d-ket, amelyek osztói n-nek. Ez bizonyítható a számelmélet alaptételével, mivel azok az értékek, amelyeket a függvény nem prímhatványokra vesz fel, csak a nulla. Legyen például n = 12 = 2² × 3. Ekkor

${\begin{aligned}\sum _{d\mid 12}\Lambda (d)&=\Lambda (1)+\Lambda (2)+\Lambda (3)+\Lambda (4)+\Lambda (6)+\Lambda (12)\\&=\Lambda (1)+\Lambda (2)+\Lambda (3)+\Lambda \left(2^{2}\right)+\Lambda (2\times 3)+\Lambda \left(2^{2}\times 3\right)\\&=0+\log(2)+\log(3)+\log(2)+0+0\\&=\log(2\times 3\times 2)\\&=\log(12).\end{aligned}}$

A Möbius-inverzióval kapjuk, hogy

$\Lambda (n)=-\sum _{d\mid n}\mu (d)\log(d)\ .$

Dirichlet-sor

A von Mangoldt-függvény fontos szerepet játszik a Dirichlet-sorok elméletében, és a Riemann-féle zéta-függvényhez is kapcsolódik. Speciálisan,

$\log \zeta (s)=\sum _{n=2}^{\infty }{\frac {\Lambda (n)}{\log(n)}}\,{\frac {1}{n^{s}}},\qquad {\text{Re}}(s)>1.$

A logaritmikus derivált

${\frac {\zeta ^{\prime }(s)}{\zeta (s)}}=-\sum _{n=1}^{\infty }{\frac {\Lambda (n)}{n^{s}}}.$

Ezek a Dirichlet-sorokkal való kapcsolat speciális esetei. Ha

$F(s)=\sum _{n=1}^{\infty }{\frac {f(n)}{n^{s}}}$

egy  f (n) teljesen multiplikatív függvény, és a sor konvergál a Re(s) > σ₀ helyekre, akkor

${\frac {F^{\prime }(s)}{F(s)}}=-\sum _{n=1}^{\infty }{\frac {f(n)\Lambda (n)}{n^{s}}}$

konvergens minden Re(s) > σ₀-ra.

Csebisev-függvény

A ψ(x) második Csebisev-függvény a von Mangoldt-függvény összegfüggvénye:

$\psi (x)=\sum _{p^{k}\leq x}\log p=\sum _{n\leq x}\Lambda (n)\ .$

A Csebisev-függvény Mellin-transzformációja a Perron-formula felhasználásával:

${\frac {\zeta ^{\prime }(s)}{\zeta (s)}}=-s\int _{1}^{\infty }{\frac {\psi (x)}{x^{s+1}}}\,dx$

ami teljesül, ha Re(s) > 1.

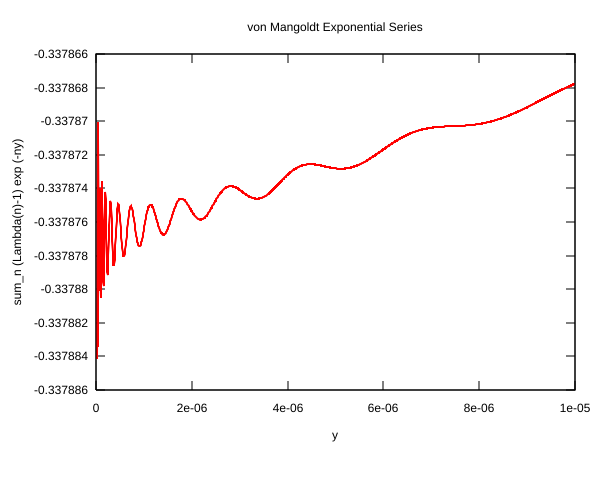
Exponenciális sorok

Hardy és Littlewood vizsgálta ennek a sornak az y → 0⁺ határértékét

$F(y)=\sum _{n=2}^{\infty }\left(\Lambda (n)-1\right)e^{-ny}$

A Riemann-hipotézis teljesülésének esetére belátták, hogy

$F(y)=O\left({\frac {1}{\sqrt {y}}}\right).$

Azt is megmutatták, hogy a sor oszcillál, mégpedig egyre erősebben. Sőt, létezik egy K > 0 úgy, hogy végtelen gyakran

$F(y)<-{\frac {K}{\sqrt {y}}},\quad {\text{ és }}\quad F(y)>{\frac {K}{\sqrt {y}}}$

A mellékelt grafikon mutatja, hogy ez az első valahány számra ez nem nyilvánvaló: az oszcilláció egészen az első 100 millió tag összegzéséig nem látható tisztán, és csak akkor látható, ha y < 10⁻⁵.

Riesz-közép

A von Mangoldt-függvény Riesz-közepe

${\begin{aligned}\sum _{n\leq \lambda }\left(1-{\frac {n}{\lambda }}\right)^{\delta }\Lambda (n)&=-{\frac {1}{2\pi i}}\int _{c-i\infty }^{c+i\infty }{\frac {\Gamma (1+\delta )\Gamma (s)}{\Gamma (1+\delta +s)}}{\frac {\zeta ^{\prime }(s)}{\zeta (s)}}\lambda ^{s}ds\\&={\frac {\lambda }{1+\delta }}+\sum _{\rho }{\frac {\Gamma (1+\delta )\Gamma (\rho )}{\Gamma (1+\delta +\rho )}}+\sum _{n}c_{n}\lambda ^{-n}.\end{aligned}}$

ahol λ és δ a Riesz-közép paraméterei, és c > 1. A ρ fölötti összeg a Riemann-féle zéta-függvény gyökei fölötti összeg, és

$\sum _{n}c_{n}\lambda ^{-n}\,$

konvergens, ha λ > 1.

Approximáció a Riemann-féle zéta-függvény gyökeivel

A Riemann-féle zéta-függvény gyökei fölötti összeg:

$-\sum _{i=1}^{\infty }n^{\rho (i)}$

ahol ρ(i) az i-edik zéta-gyök, a csúcsok a prímeknél, ami numerikus számításokkal is bizonyítható. Az összeg nem megy el addig, hogy kiadja a von Mangoldt-függvény értékeit.

A von Mangoldt-függvény Fourier-transzformációja által adott spektrumban a csúcsok a Riemann-féle zéta-függvény gyökeinek képzetes részeinél vannak. Ezt néha dualitásnak nevezik.

A von Mangoldt-függvény Fourier-transzformáltja

Források

• * Apostol, Tom M. (1976), Introduction to analytic number theory, Undergraduate Texts in Mathematics, New York-Heidelberg: Springer-Verlag, ISBN 978-0-387-90163-3
• Tenebaum, Gérald. Introduction to analytic and probabilistic number theory, Translated by C.B. Thomas, Cambridge Studies in Advanced Mathematics, Cambridge: Cambridge University Press (1995). ISBN 0-521-41261-7