Arg max

As an example, both unnormalised and normalised sinc functions above have arg max of {0} because both attain their global maximum value of 1 at x = 0.

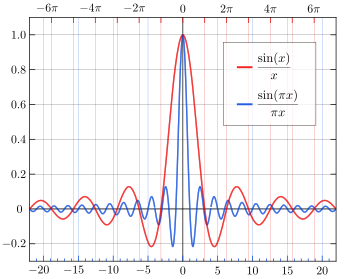
The unnormalised sinc function (red) has arg min of {−4.49, 4.49}, approximately, because it has 2 global minimum values of approximately −0.217 at x = ±4.49. However, the normalised sinc function (blue) has arg min of {−1.43, 1.43}, approximately, because their global minima occur at x = ±1.43, even though the minimum value is the same.

In mathematics, the arguments of the maxima (abbreviated arg max or argmax) are the points of the domain of some function at which the function values are maximized. In contrast to global maxima, referring to the largest outputs of a function, arg max refers to the inputs, or arguments, at which the function outputs are as large as possible.

Definition

Given an arbitrary set X, a totally ordered set Y, and a function, $f\colon X\rightarrow Y$, the arg max over some subset, S, of X is defined by

${\underset {x\in S\subseteq X}{\operatorname {arg\,max} }}\,f(x):=\{x\mid x\in S\wedge \forall y\in S:f(y)\leq f(x)\}.$

If S = X or S is clear from the context, then S is often left out, as in ${\underset {x}{\operatorname {arg\,max} }}\,f(x):=\{x\mid \forall y:f(y)\leq f(x)\}.$ In other words, arg max is the set of points, x, for which f(x) attains the function's largest value (if it exists). Arg max may be the empty set, a singleton, or contain multiple elements. For example, if f(x) is 1−|x|, then f attains its maximum value of 1 only at the point x = 0. Thus,

${\underset {x}{\operatorname {arg\,max} }}\,(1-|x|)=\{0\}$.

The arg max operator is to be distinguished from the max operator which, given the same function, returns the maximum value instead of the point or points that reach that value; in other words

$\max _{x}f(x)$ is the element in $\{f(x)\mid \forall y:f(y)\leq f(x)\}.$

Like arg max, max may be the empty set (in which case the maximum is undefined) or a singleton, but unlike arg max, max may not contain multiple elements: for example, if f(x) is 4x² − x⁴, then ${\underset {x}{\operatorname {arg\,max} }}\,\left(4x^{2}-x^{4}\right)=\left\{-{\sqrt {2}},{\sqrt {2}}\right\}$, but ${\underset {x}{\operatorname {max} }}\,\left(4x^{2}-x^{4}\right)=\{4\}$ because the function attains the same value at every element of arg max.

Equivalently, if M is the maximum of f, then the arg max is the level set of the maximum:

${\underset {x}{\operatorname {arg\,max} }}\,f(x)=\{x\mid f(x)=M\}=:f^{-1}(M)$

We can rearrange to give the simple identity

$f\left({\underset {x}{\operatorname {arg\,max} }}\,f(x)\right)=\max _{x}f(x)$.

If the maximum is reached at a single point then this point is often referred to as the arg max, and arg max is considered a point, not a set of points. So, for example,

${\underset {x\in \mathbb {R} }{\operatorname {arg\,max} }}\,(x(10-x))=5$

(rather than the singleton set {5}), since the maximum value of x(10 − x) is 25, which occurs for x = 5. However, in case the maximum is reached at many points, arg max needs to be considered a set of points.

For example

${\underset {x\in [0,4\pi ]}{\operatorname {arg\,max} }}\,\cos(x)=\{0,2\pi ,4\pi \}$

since the maximum value of cos(x) is 1, which occurs on this interval for x = 0, 2π or 4π. On the whole real line

${\underset {x\in \mathbb {R} }{\operatorname {arg\,max} }}\,\cos(x)=\{2k\pi :k\in \mathbb {Z} \}$, so an infinite set.

Functions need not in general attain a maximum value, and hence the arg max is sometimes the empty set; for example, ${\underset {x\in \mathbb {R} }{\operatorname {arg\,max} }}\,x^{3}=\emptyset$, since $x^{3}$ is unbounded on the real line. As another example, ${\underset {x\in \mathbb {R} }{\operatorname {arg\,max} }}\,\arctan(x)=\emptyset$, although arc tan is bounded by ±π/2. However, by the extreme value theorem, a continuous real-valued function on a closed interval has a maximum, and thus a nonempty arg max.

Arg min

arg min (or argmin) stands for argument of the minimum, and is defined analogously. For instance,

${\underset {x}{\operatorname {arg\,min} }}\,f(x):=\{x\mid x\in S\wedge \forall y\in S:f(y)\geq f(x)\}$

are points x for which f(x) attains its smallest value. It is the complementary operator of $arg\,max$.

See also

• Argument of a function
• Maxima and minima
• Mode (statistics)
• Mathematical optimization
• Kernel (linear algebra)
• Preimage

External links

• arg min and arg max at PlanetMath.org.