BQP
In computational complexity theory, bounded-error quantum polynomial time (BQP) is the class of decision problems solvable by a quantum computer in polynomial time, with an error probability of at most 1/3 for all instances[1]. It is the quantum analogue of the complexity class BPP.
A decision problem is a member of BQP if there exists a quantum algorithm (an algorithm that runs on a quantum computer) that solves the decision problem with high probability and is guaranteed to run in polynomial time. A run of the algorithm will correctly solve the decision problem with a probability of at least 2/3.
| BQP algorithm (1 run) | ||
|---|---|---|
Answer produced Correct
answer |
Yes | No |
| Yes | ≥ 2/3 | ≤ 1/3 |
| No | ≤ 1/3 | ≥ 2/3 |
| BQP algorithm (k runs) | ||
Answer producedCorrect
answer |
Yes | No |
| Yes | > 1 − 2−ck | < 2−ck |
| No | < 2−ck | > 1 − 2−ck |
| for some constant c > 0 | ||
Contents
Definition[edit]
BQP can be viewed as the languages associated with certain bounded-error uniform families of quantum circuits[1]. A language L is in BQP if and only if there exists a polynomial-time uniform family of quantum circuits , such that
- For all , Qn takes n qubits as input and outputs 1 bit
- For all x in L,
- For all x not in L,
Alternatively, one can define BQP in terms of quantum Turing machines. A language L is in BQP if and only if there exists a polynomial quantum Turing machine that accepts L with an error probability of at most 1/3 for all instances.[2]
Similarly to other "bounded error" probabilistic classes the choice of 1/3 in the definition is arbitrary. We can run the algorithm a constant number of times and take a majority vote to achieve any desired probability of correctness less than 1, using the Chernoff bound. The complexity class is unchanged by allowing error as high as 1/2 − n−c on the one hand, or requiring error as small as 2−nc on the other hand, where c is any positive constant, and n is the length of input.[3]
Quantum computation[edit]
The number of qubits in the computer is allowed to be a polynomial function of the instance size. For example, algorithms are known for factoring an n-bit integer using just over 2n qubits (Shor's algorithm).
Usually, computation on a quantum computer ends with a measurement. This leads to a collapse of quantum state to one of the basis states. It can be said that the quantum state is measured to be in the correct state with high probability.
Quantum computers have gained widespread interest because some problems of practical interest are known to be in BQP, but suspected to be outside P. Some prominent examples are:
- Integer factorization (see Shor's algorithm)[4]
- Discrete logarithm[4]
- Simulation of quantum systems (see universal quantum simulator)
- Approximating the Jones polynomial at certain roots of unity
Relationship to other complexity classes[edit]
| Unsolved problem in computer science: What is the relationship between BQP and NP? (more unsolved problems in computer science)
|
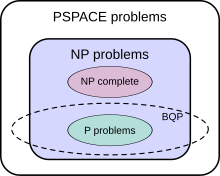
This class is defined for a quantum computer and its natural corresponding class for an ordinary computer (or a Turing machine plus a source of randomness) is BPP. Just like P and BPP, BQP is low for itself, which means BQPBQP = BQP[2]. Informally, this is true because polynomial time algorithms are closed under composition. If a polynomial time algorithm calls as a subroutine polynomially many polynomial time algorithms, the resulting algorithm is still polynomial time.
BQP contains P and BPP and is contained in AWPP,[5] PP[6] and PSPACE.[2] In fact, BQP is low for PP, meaning that a PP machine achieves no benefit from being able to solve BQP problems instantly, an indication of the possible difference in power between these similar classes. The known relationships with classic complexity classes are:
As the problem of P ≟ PSPACE has not yet been solved, the proof of inequality between BQP and classes mentioned above is supposed to be difficult.[2] The relation between BQP and NP is not known. In May 2018, computer scientists Ran Raz of Princeton University and Avishay Tal of Stanford University published a paper[7] which showed that, relative to an oracle, BQP was not contained in PH.
Adding postselection to BQP results in the complexity class PostBQP which is equal to PP.[8][9]
See also[edit]
- Hidden subgroup problem
- Polynomial hierarchy (PH).
- Quantum complexity theory, mainly P and NP.
References[edit]
- ^ a b c Michael Nielsen and Isaac Chuang (2000). Quantum Computation and Quantum Information. Cambridge: Cambridge University Press. ISBN 0-521-63503-9.
- ^ a b c d Bernstein, Ethan; Vazirani, Umesh (October 1997). "Quantum Complexity Theory". SIAM Journal on Computing. 26 (5): 1411–1473. doi:10.1137/S0097539796300921. Retrieved 23 July 2018.
- ^ Barak, Sanjeev Arora, Boaz (2009). Computational Complexity: A Modern Approach / Sanjeev Arora and Boaz Barak. Cambridge. p. 122. Retrieved 24 July 2018.
- ^ a b arXiv:quant-ph/9508027v2 Polynomial-Time Algorithms for Prime Factorization and Discrete Logarithms on a Quantum Computer, Peter W. Shor
- ^ Fortnow, Lance; Rogers, John (1999). "Complexity limitations on Quantum computation" (PDF). J. Comput. Syst. Sci. Boston, MA: Academic Press. 59 (2): 240–252. doi:10.1006/jcss.1999.1651. ISSN 0022-0000.
- ^ L. Adleman, J. DeMarrais, and M.-D. Huang. Quantum computability. SIAM J. Comput., 26(5):1524–1540, 1997.
- ^ George, Michael Goderbauer, Stefan. "ECCC - TR18-107". eccc.weizmann.ac.il. Retrieved 2018-08-03.
- ^ Aaronson, Scott (2005). "Quantum computing, postselection, and probabilistic polynomial-time". Proceedings of the Royal Society A. 461 (2063): 3473–3482. arXiv:quant-ph/0412187. Bibcode:2005RSPSA.461.3473A. doi:10.1098/rspa.2005.1546.. Preprint available at [1]
- ^ Aaronson, Scott (2004-01-11). "Complexity Class of the Week: PP". Computational Complexity Weblog. Retrieved 2008-05-02.