Runge–Kutta-módszer

A Runge–Kutta-módszerek családja a differenciálegyenletek numerikus analízisének széles körben ismert és alkalmazott közelítő eljárása, amelyet Carl Runge és Martin Kutta német matematikusok dolgoztak ki 1900 körül.

A közönséges negyedrendű Runge–Kutta-módszer

A Runge–Kutta-módszercsalád közönséges negyedrendű tagja annyira elterjedten használatos, hogy egyszerűen csak „a Runge–Kutta-módszer”-ként hivatkoznak rá. E módszer az alábbi kezdetiérték-probléma egy negyedrendű közelítő megoldását adja.

$y'(t)=f(\;t\;,\;y(t)\;)\qquad y(t_{0})=y_{0}$

Azaz tetszőlegesen rögzített pozitív valós, tipikus esetben kicsiny $h$ lépésköz esetén az $n$-edik lépésben a kezdetiérték-probléma $y(t)$ megoldásának egy olyan

$y(t_{n})\;\approx \;y_{n}$

közelítését adja a

$t_{n}=t_{0}+n\cdot h$

helyen, amely közelítés hibája negyedrendű. E negyedrendűség azt jelenti, hogy a választott lépésköz zsugorításakor annak negyedik hatványával zsugorodik a hibára adott felső becslés. Például a lépésköz harmadolása árán, azaz nagyjából háromszor annyi számolás árán a hibakorlát $(1/3)^{4}=1/81$-szeresre zsugorodik.

A $h$ lépésköz rögzítése után az alábbi, $n$-szerinti rekurziós lépésekkel kapjuk az $y(t)$ megoldásfüggvény közelítését.

${\begin{aligned}y_{n+1}&=y_{n}+h\cdot {a_{n}+2\cdot b_{n}+2\cdot c_{n}+d_{n} \over 6}\\{\text{ahol}}\\a_{n}&=f(\;t_{n}\;,\;y_{n}\;)\\b_{n}&=f(\;t_{n}+{\tfrac {1}{2}}h\;,\;y_{n}+{\tfrac {1}{2}}h\cdot a_{n}\;)\\c_{n}&=f(\;t_{n}+{\tfrac {1}{2}}h\;,\;y_{n}+{\tfrac {1}{2}}h\cdot b_{n}\;)\\d_{n}&=f(\;t_{n}+h\;,\;y_{n}+h\cdot c_{n}\;)\end{aligned}}$

Így, a $t_{n+1}$ helyhez tartozó $y_{n+1}$ közelítőérték egyenlő a $t_{n}$ helyhez tartozó $y_{n}$ közelítőérték, plusz a becsült meredekség szorozva az intervallum $h$ hosszával. A meredekség becslése egy, most nem részletezett matematikai megfontolás alapján súlyozott középértéke az alábbi négy meredekségi becslésnek:

${\begin{aligned}a_{n}&=f(\;t_{n}\;,\;y_{n}\;)\\&\approx f(\;t_{n}\;,\;y(t_{n})\;)\\&=y'(t_{n})\\b_{n}&=f(\;t_{n}+{\tfrac {1}{2}}h\;,\;y_{n}+{\tfrac {1}{2}}h\cdot a_{n}\;)\\&\approx f(\;t_{n}+{\tfrac {1}{2}}h\;,\;y(t_{n})+{\tfrac {1}{2}}h\cdot y'(t_{n})\;)\\&\approx f(\;t_{n}+{\tfrac {1}{2}}h\;,\;y(t_{n}+{\tfrac {1}{2}}h)\;)\\&=y'(t_{n}+{\tfrac {1}{2}}h)\\c_{n}&=f(\;t_{n}+{\tfrac {1}{2}}h\;,\;y_{n}+{\tfrac {1}{2}}h\cdot b_{n}\;)\\&\approx f(\;t_{n}+{\tfrac {1}{2}}h\;,\;y(t_{n})+{\tfrac {1}{2}}h\cdot y'(t_{n}+{\tfrac {1}{2}}h)\;)\\&\approx f(\;t_{n}+{\tfrac {1}{2}}h\;,\;y(t_{n}+{\tfrac {1}{2}}h)\;)\\&=y'(t_{n}+{\tfrac {1}{2}}h)\\d_{n}&=f(\;t_{n}+h\;,\;y_{n}+h\cdot c_{n}\;)\\&\approx f(\;t_{n}+h\;,\;y(t_{n})+h\cdot y'(t_{n}+{\tfrac {1}{2}}h)\;)\\&\approx f(\;t_{n}+h\;,\;y(t_{n}+h)\;)\\&=y'(t_{n}+h)\end{aligned}}$

E négy közelítés átlagolásánál a $t_{n}$ és $t_{n+1}$ szélekhez képest a $t_{n+0.5}$ felezőnél dupla súlyt alkalmazunk.

${\begin{aligned}{\mbox{átlagos meredekség}}&\;\approx \;{y'(t_{n})+2\cdot y'(t_{n}+{\tfrac {1}{2}}h)+2\cdot y'(t_{n}+{\tfrac {1}{2}}h)+y'(t_{n}+h) \over 6}\\&\;\approx \;{1\cdot a_{n}+2\cdot b_{n}+2\cdot c_{n}+1\cdot d_{n} \over 6}\end{aligned}}$

Mivel a megoldásfüggvény felvett értékeire csak additív műveleteket és a skalárral való szorzás műveletét alkalmazzuk, lényegében ezért a módszer nem csak skalár értékű megoldásfüggvények, hanem vektor értékűek esetén is alkalmazható. Ilyen például a Schrödinger-differenciálegyenlet, amelynek Hamilton-operátorát használjuk a fenti szerepében.

Explicit Runge–Kutta-módszer

A fent említett Runge–Kutta-módszercsalád általánosítása az explicit Runge–Kutta-módszer, amit a

$y_{n+1}=y_{n}+h\sum _{i=1}^{s}b_{i}k_{i},$

ad meg, ahol

$k_{1}=f(t_{n},y_{n}),\,$

$k_{2}=f(t_{n}+c_{2}h,y_{n}+a_{21}hk_{1}),\,$

$k_{3}=f(t_{n}+c_{3}h,y_{n}+a_{31}hk_{1}+a_{32}hk_{2}),\,$

$\vdots$

$k_{s}=f(t_{n}+c_{s}h,y_{n}+a_{s1}hk_{1}+a_{s2}hk_{2}+\cdots +a_{s,s-1}hk_{s-1}).$

(Megjegyzés: a fenti egyenletek különböző formákban is megjelenhetnek egyéb forrásokból, de jelentésük azonos).

Ahhoz hogy meghatározzunk egy bizonyos módszert,kell egy s egész változó (a szakaszok száma), illetve az a_ij (1 ≤ j < i ≤ s), b_i (i = 1, 2, ..., s) és a c_i (i = 2, 3, ..., s) együtthatók. Ezek az adatok általában egy mnemonik eszközbe kerülnek be, ami a Butcher táblájaként ismert (Butcher tableau, John C. Butcher neve után):

	0
	$c_{2}$	$a_{21}$
	$c_{3}$	$a_{31}$	$a_{32}$
	$\vdots$	$\vdots$		$\ddots$
	$c_{s}$	$a_{s1}$	$a_{s2}$	$\cdots$	$a_{s,s-1}$
		$b_{1}$	$b_{2}$	$\cdots$	$b_{s-1}$	$b_{s}$

A Runge-Kutta-módszer konzisztens, ha

$\sum _{j=1}^{i-1}a_{ij}=c_{i}\ \mathrm {ha} \ i=2,\ldots ,s.$

Ugyanakkor vannak más követelmények, ha azt szeretnénk, hogy a módszernek legyen p fokszáma, így a kerekítési hiba O(h^p+1) lesz. Például egy kétlépcsős módszer másodrendű ha b₁ + b₂ = 1, b₂c₂ = 1/2, és b₂a₂₁ = 1/2.

Példák

A RK4 szerkezete a következő táblázat szerint értelmezhető:

	0
	1/2	1/2
	1/2	0	1/2
	1	0	0	1
		1/6	1/3	1/3	1/6

Habár a legegyszerűbb Runga-Kutta-módszer az Euler-módszer maga, amelynek $y_{n+1}=y_{n}+hf(t_{n},y_{n})$ képlet ad meg. Ez az egyetlen explicit Runge-Kutta-módszer egy lépcsővel.

	0
		1

Egy példa a másodrendű két lépcsős módszerre a középponti módszer:

$y_{n+1}=y_{n}+hf\left(t_{n}+{\tfrac {1}{2}}h,y_{n}+{\tfrac {1}{2}}hf(t_{n},y_{n})\right).$

Az erre megfelelő táblázat:

	0
	1/2	1/2
		0	1

Megjegyzendő, a középponti módszer nem a legmegfelelőbb RK-módszer. A Heun-módszer egy alternatív megoldást kínál, ahol a tábla 1/2-ei 1-re cserélődnek, és a b sora pedig [1/2,1/2]. Ha valaki minimalizálni akarja a kerekítés által keletkezett hibákat, akkor az alábbi módszert kell használnia (Atkinson p. 423). Más fontos módszerek: Fehlberg, Cash-Karp és Dormand-Prince.

Használat

A következő egy példa a kétlépcsős explicit Runge-Kutta-módszerre:

	0
	2/3	2/3
		1/4	3/4

a kezdeti értéket meghatározó képlet

$y'=\tan(y)+1,\quad y(1)=1,\ t\in [1,1.1]$

a h=0,025 lépésköz

A fenti táblát meghatározó egyenrangú számítások:

$k_{1}=y_{n}$

$k_{2}=y_{n}+{\tfrac {2}{3}}hf(t_{n},k_{1})$

$y_{n+1}=y_{n}+h\left({\tfrac {1}{4}}f(t_{n},k_{1})+{\tfrac {3}{4}}f(t_{n}+{\tfrac {2}{3}}h,k_{2})\right)$

$t_{0}=1$
	$y_{0}=1$
$t_{1}=1.025$
	$k_{1}=y_{0}=1$	$f(t_{0},k_{1})=2.557407725$	$k_{2}=y_{0}+2/3hf(t_{0},k_{1})=1.042623462$
	$y_{1}=y_{0}+h(1/4*f(t_{0},k_{1})+3/4*f(t_{0}+2/3h,k_{2}))=1.066869388$
$t_{2}=1.05$
	$k_{1}=y_{1}=1.066869388$	$f(t_{1},k_{1})=2.813524695$	$k_{2}=y_{1}+2/3hf(t_{1},k_{1})=1.113761467$
	$y_{2}=y_{1}+h(1/4*f(t_{1},k_{1})+3/4*f(t_{1}+2/3h,k_{2}))=1.141332181$
$t_{3}=1.075$
	$k_{1}=y_{2}=1.141332181$	$f(t_{2},k_{1})=3.183536647$	$k_{2}=y_{2}+2/3hf(t_{2},k_{1})=1.194391125$
	$y_{3}=y_{2}+h(1/4*f(t_{2},k_{1})+3/4*f(t_{2}+2/3h,k_{2}))=1.227417567$
$t_{4}=1.1$
	$k_{1}=y_{3}=1.227417567$	$f(t_{3},k_{1})=3.796866512$	$k_{2}=y_{3}+2/3hf(t_{3},k_{1})=1.290698676$
	$y_{4}=y_{3}+h(1/4*f(t_{3},k_{1})+3/4*f(t_{3}+2/3h,k_{2}))=1.335079087$

Az aláhúzott kifejezések jelzik a számszerû megoldásokat.Megjegyzendõ, az $y_{i}$s újraszámolása érdekében $f(t_{i},k_{1})$-et használtunk.

Adaptív Runge–Kutta-módszer

Az adaptív módszer arra volt tervezve, hogy megadja a becsült helyi kerekítési hibát minden egyes RK lépésben. Ezt úgy valósította meg, hogy két módszert tartalmaz a táblázat, egyet p-ed rendűvel és egyet p-1-ed rendűvel.

A kisebb rendű lépés adott:

$y_{n+1}^{*}=y_{n}+h\sum _{i=1}^{s}b_{i}^{*}k_{i},$

ahol, a $k_{i}$ megegyezik a magasabb rendű módszerrel. Ekkor a hiba:

$e_{n+1}=y_{n+1}-y_{n+1}^{*}=h\sum _{i=1}^{s}(b_{i}-b_{i}^{*})k_{i},$

ami $O(h^{p})$. A Butcher-táblázat erre a módszerre ki van bővítve, így megadja a $b_{i}^{*}$ értékeit:

	0
	$c_{2}$	$a_{21}$
	$c_{3}$	$a_{31}$	$a_{32}$
	$\vdots$	$\vdots$		$\ddots$
	$c_{s}$	$a_{s1}$	$a_{s2}$	$\cdots$	$a_{s,s-1}$
		$b_{1}$	$b_{2}$	$\cdots$	$b_{s-1}$	$b_{s}$
		$b_{1}^{*}$	$b_{2}^{*}$	$\cdots$	$b_{s-1}^{*}$	$b_{s}^{*}$

A RK Fehlberg módszernek a két rendszere az ötöd- és negyedrendű. Ennek a kibővített Butcher-táblázata a következő:

	0
	1/4	1/4
	3/8	3/32	9/32
	12/13	1932/2197	−7200/2197	7296/2197
	1	439/216	−8	3680/513	-845/4104
	1/2	−8/27	2	−3544/2565	1859/4104	−11/40
		16/135	0	6656/12825	28561/56430	−9/50	2/55
		25/216	0	1408/2565	2197/4104	−1/5	0

Habár a legegyszerűbb adaptív Runge–Kutta-módszer a másodrendű Heun-módszert és az elsőrendű Euler-módszert foglalja magába. Ennek a kibővített Butcher-táblázata:

	0
	1	1
		1/2	1/2
		1	0

A hiba eredményét a lépték határozza meg.

Más adaptiv Runge-Kutta-módszerek a Bogacki-Shampine-módszer (harmad-és másodrendű), a Cash-Karp-módszer és a Dormand-Prince-módszer (mindkettő ötöd- és negyedrendű).

Implicit Runge-Kutta-módszer

Az implicit módszerek jóval általánosabbak az expliciteknél. Az eltérés a Butcher-táblázatnál merül fel: az implicit módszernél, a mátrix a_ij együtthatója nem feltétlenül alacsony háromszög:

${\begin{array}{c|cccc}c_{1}&a_{11}&a_{12}&\dots &a_{1s}\\c_{2}&a_{21}&a_{22}&\dots &a_{2s}\\\vdots &\vdots &\vdots &\ddots &\vdots \\c_{s}&a_{s1}&a_{s2}&\dots &a_{ss}\\\hline &b_{1}&b_{2}&\dots &b_{s}\\\end{array}}={\begin{array}{c|c}\mathbf {c} &A\\\hline &\mathbf {b^{T}} \\\end{array}}$

A megközelítő megoldás a kezdeti érték problémára utal az együtthatók nagyobb számára.

$y_{n+1}=y_{n}+h\sum _{i=1}^{s}b_{i}k_{i}\,$

$k_{i}=f\left(t_{n}+c_{i}h,y_{n}+h\sum _{j=1}^{s}a_{ij}k_{j}\right).$

Az $a_{ij}$ mátrix telítettsége miatt, az egyes $k_{i}$ becslése jelentékeny mértékben fog függeni az $f(t,y)$ függvénytől. A nehézségek ellenére, az implicit módszerek nagy jelentőséggel birnak az erősen stabil állapotuk miatt, ami különösen fontos a parciális differenciál egyenletek megoldásában. A legegyszerűbb példa egy implicit Runge-Kutta-módszerre fordított Euler-módszer:

$y_{n+1}=y_{n}+hf(t_{n}+h,y_{n+1})\,$

Ennek táblázata egyszerű:

${\begin{array}{c|c}1&1\\\hline &1\\\end{array}}$

Még az egyszerűbb implicit módszer alkalmazása is bonyolulttá válhat, ami a ki kifejezésből látszik is:

$k_{1}=f(t_{n}+c_{1}h,y_{n}+ha_{11}k_{1})\rightarrow k_{1}=f(t_{n}+h,y_{n}+hk_{1}).$

Ebben az esetben, a fenti bonyolult kifejezés leegyszerűsíthető a következőképpen:

$y_{n+1}=y_{n}+hk_{1}\rightarrow hk_{1}=y_{n+1}-y_{n}\,$

így hát

$k_{1}=f(t_{n}+h,y_{n}+y_{n+1}-y_{n})=f(t_{n}+h,y_{n+1}).\,$

amiből következik, hogy:

$y_{n+1}=y_{n}+hf(t_{n}+h,y_{n+1})\,$

Noha egyszerűbb, mint a módosítások előtti „nyers” kifejezés, ez egy implicit összefüggés, tehát a konkrét megoldás problémafüggő. A többlépéses implicit módszert sikeresen használják a kutatók. Az egyensúly összeállítása (kombinációja), a magasabb rendpontosság kevesebb lépésben és a léphetőség (stepping) egyedül az előző értékben válik érdekessé, ugyanakkor a bonyolult példa jellegzetes kivitelezése, és a tény, hogy ki ismételt megközelítései mutatják hogy ezek hasonlóak (ugyanazok).

Algoritmus

Legyen mondjuk a $y^{'}(x)=-2*y(x);y(0)=3$ differenciálegyenlet, aminek a megoldása:$y(x)=3*e^{-2*x}$

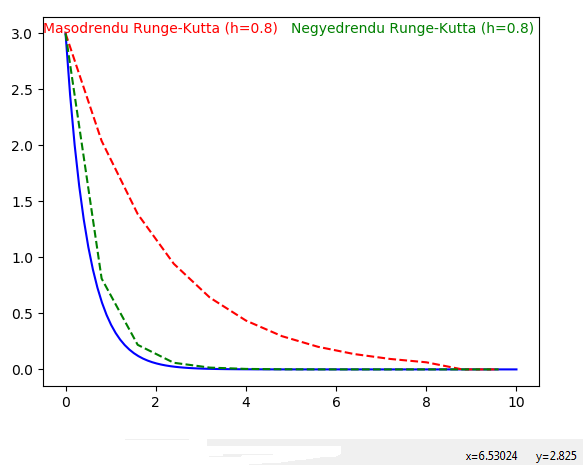
import math
import numpy as np
import matplotlib.pyplot as plt

x0=0
y0=3
h=0.8
def ypontos():
	x=np.linspace(0,10,100)
	y=3*np.exp(-2*x)
	plt.plot(x,y,"-b")
def f(x, y):
	return(-2*y)
def RungeKutta2nd(f, h, x0, y0):
	x=np.arange(0, 10, h)
	y=x*0
	y[0]=y0
	for i in range(10):
		k1=h*f(x[i],y[i])
		k2=h*f(x[i]+h/2,y[i]+k1/2)
		y[i+1]=y[i]+k2
	plt.plot(x,y, "--r")
	plt.text(-0.5, 3,'Masodrendu Runge-Kutta (h=0.8)',color='red', fontsize=10)
def RungeKutta4th(f, h, x0, y0):
	x=np.arange(0, 10, h)
	y=x*0
	y[0]=y0
	for i in range(10):
		k1=h*f(x[i],y[i])
		k2=h*f(x[i]+h/2,y[i]+k1/2)
		k3=h*f(x[i]+h/2,y[i]+k2/2)
		k4=h*f(x[i]+h,y[i]+k3)
		y[i+1]=y[i]+(k1+2*k2+2*k3+k4)/6
	plt.plot(x,y, "--g")
	plt.text(5, 3,'Negyedrendu Runge-Kutta (h=0.8)',color='green', fontsize=10)
ypontos()
RungeKutta2nd(f, h, x0, y0)
RungeKutta4th(f, h, x0, y0)
plt.show()

A program lefuttatása után egy grafikonon összehasonlíthatjuk a másodrendű illetve 4.-edrendű Runge-Kutta módszereket illetve a tényleges megoldást.