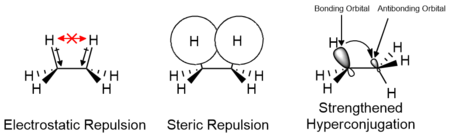Conformational isomerism

From Wikipedia, the free encyclopedia
Jump to navigation Jump to search
Rotation about single bond of butane to interconvert one conformation to another. The gauche conformation on the right is a conformer, while the eclipsed conformation on the left is a transition state between conformers. Above: Newman projection; below: depiction of spatial orientation.

In chemistry, conformational isomerism is a form of stereoisomerism in which the isomers can be interconverted just by rotations about formally single bonds (refer to figure on single bond rotation). While any two arrangements of atoms in a molecule that differ by rotation about single bonds can be referred to as different conformations, conformations that correspond to local minima on the energy surface are specifically called conformational isomers or conformers.[1] Rotations about single bonds involve overcoming a rotational energy barrier to interconvert one conformer to another. If the energy barrier is low, there is free rotation[2] and a sample of the compound exists as a mixture of multiple conformers; if the energy barrier is high enough then there is restricted rotation, a molecule may exist for a relatively long time period as a stable rotational isomer or rotamer (an isomer arising from hindered single-bond rotation). When the time scale for interconversion is long enough for isolation of individual rotamers (usually arbitrarily defined as a half-life of interconversion of 1000 seconds or longer), the isomers are termed atropisomers (see: atropisomerism).[1][3][4] The ring-flip of substituted cyclohexanes constitutes another common form of conformational isomerism.

Conformational isomers are thus distinct from the other classes of stereoisomers (i. e. configurational isomers) where interconversion necessarily involves breaking and reforming of chemical bonds.[5] For example, L/D- and R/S- configurations of organic molecules have different handedness and optical activities, and can only be interconverted by breaking one or more bonds connected to the chiral atom and reforming a similar bond in a different direction or spatial orientation. They also differ from geometric (cis/trans) isomers, another class of stereoisomers, which require the π-component of double bonds to break for interconversion. (Although the distinction is not always clear-cut, since certain bonds that are formally single bonds actually have double bond character that becomes apparent only when secondary resonance contributors are considered, like the C–N bonds of amides, for instance.) Due to rapid interconversion, conformers are usually not isolable at room temperature.

The study of the energetics between different conformations is referred to as conformational analysis.[6] It is useful for understanding the stability of different isomers, for example, by taking into account the spatial orientation and through-space interactions of substituents. In addition, conformational analysis can be used to predict and explain product selectivity, mechanisms, and rates of reactions.[7]

Types[edit]

Relative conformation energy diagram of butane as a function of dihedral angle.[8] A: antiperiplanar, anti or trans. B: synclinal or gauche. C: anticlinal or eclipsed. D: synperiplanar or cis.[1]

The types of conformational isomers are related to the spatial orientations of the substituents between two vicinal atoms. These are eclipsed and staggered. The staggered conformation includes the gauche (±60°) and anti (180°) conformations, depending on the spatial orientations of the two substituents.

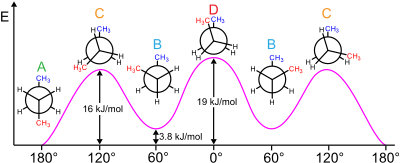
For example, butane has three conformers relating to its two methyl (CH3) groups: two gauche conformers, which have the methyls ±60° apart and are enantiomeric, and an anti conformer, where the four carbon centres are coplanar and the substituents are 180° apart (refer to free energy diagram of butane). The energy difference between gauche and anti is 0.9 kcal/mol associated with the strain energy of the gauche conformer. The anti conformer is, therefore, the most stable (≈ 0 kcal/mol). The three eclipsed conformations with dihedral angles of 0°, 120°, and 240° are not considered to be conformers, but are instead transition states between two conformers.[6] Note that the two eclipsed conformations have different energies: at 0° the two methyl groups are eclipsed, resulting in higher energy (≈ 5 kcal/mol) than at 120°, where the methyl groups are eclipsed with hydrogens (≈ 3.5 kcal/mol).[9]

While simple molecules can be described by these types of conformations, more complex molecules require the use of the Klyne–Prelog system to describe the different conformers.[6]

More specific examples of conformational isomerism are detailed elsewhere:

  • Ring conformation
  • Allylic strain – energetics related to rotation about the single bond between an sp2 carbon and an sp3 carbon.
  • Atropisomerism – due to restricted rotation about a bond.
  • Folding, including the secondary and tertiary structure of biopolymers (nucleic acids and proteins).
  • Akamptisomerism – due to restricted inversion of a bond angle.

Free energy and equilibria of conformational isomers[edit]

Equilibrium of conformers[edit]

Equilibrium distribution of two conformers at different temperatures given the free energy of their interconversion.

Conformational isomers exist in a dynamic equilibrium, where the relative free energies of isomers determines the population of each isomer and the energy barrier of rotation determines the rate of interconversion between isomers:[10]

,

where K is the equilibrium constant, ΔG° is the difference in standard free energy between the two conformers in kcal/mol, R is the universal gas constant (1.987×10-3 kcal/mol K), and T is the system's temperature in kelvins. In units of kcal/mol at 298 K,

.

Thus, every 1.36 kcal/mol corresponds to a factor of about 10 in term of equilibrium constant at temperatures around room temperature. (The "1.36 rule" is useful in general for estimation of equilibrium constants at room temperature from free energy differences. At lower temperatures, a smaller energy difference is needed to obtain a given equilibrium constant.)

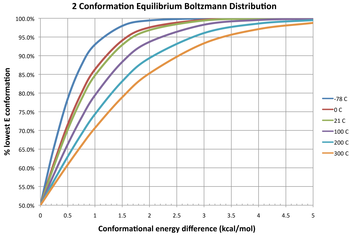
Three isotherms are given in the diagram depicting the equilibrium distribution of two conformers at different temperatures. At a free energy difference of 0 kcal/mol, this gives an equilibrium constant of 1, meaning that two conformers exist in a 1:1 ratio. The two have equal free energy; neither is more stable, so neither predominates compared to the other. A negative difference in free energy means that a conformer interconverts to a thermodynamically more stable conformation, thus the equilibrium constant will always be greater than 1. For example, the ΔG° for the transformation of butane from the gauche conformer to the anti conformer is −0.47 kcal/mol at 298 K.[11] This gives an equilibrium constant is about 2.2 in favor of the anti conformer, or a 31:69 mixture of gauche:anti conformers at equilibrium. Conversely, a positive difference in free energy means the conformer already is the more stable one, so the interconversion is an unfavorable equilibrium (K < 1). Even for highly unfavorable changes (large positive ΔG°), the equilibrium constant between two conformers can be increased by increasing the temperature, so that the amount of the less stable conformer present at equilibrium increases (although it always remains the minor conformer).

Population distribution of conformers[edit]

Boltzmann distribution % of lowest energy conformation in a two component equilibrating system at various temperatures (°C, color) and energy difference in kcal/mol (x-axis)

The fractional population distribution of different conformers follows a Boltzmann distribution:[12]

.

The left hand side is the proportion of conformer i in an equilibrating mixture of M conformers in thermodynamic equilibrium. On the right side, Ek (k = 1, 2, ..., M) is the energy of conformer k, R is the molar ideal gas constant (approximately equal to 8.314 J/(mol·K) or 1.987 cal/(mol·K)), and T is the absolute temperature. The denominator of the right side is the partition function.

Factors contributing to the free energy of conformers[edit]

The effects of electrostatic and steric interactions of the substituents as well as orbital interactions such as hyperconjugation are responsible for the relative stability of conformers and their transition states. The contributions of these factors vary depending on the nature of the substituents and may either contribute positively or negatively to the energy barrier. Computational studies of small molecules such as ethane suggest that electrostatic effects make the greatest contribution to the energy barrier; however, the barrier is traditionally attributed primarily to steric interactions.[13][14]

Contributions to rotational energy barrier

In the case of cyclic systems, the steric effect and contribution to the free energy can be approximated by A values, which measure the energy difference when a substituent is in the axial or equatorial position.

Isolation or observation of the conformational isomers[edit]

The short timescale of interconversion precludes the separation of conformational isomers in many cases. Atropisomers are conformational isomers which can be separated due to restricted rotation.[15]

Protein folding also generates stable conformational isomers which can be observed. The Karplus equation relates the dihedral angle of vicinal protons to their J-coupling constants as measured by NMR. The equation aids in the elucidation of protein folding as well as the conformations of other rigid aliphatic molecules.[16]

The equilibrium between conformational isomers may also be observed using spectroscopic techniques:

In cyclohexane derivatives, the two chair conformers interconvert with rapidly at room temperature, with cyclohexane itself undergoing the ring-flip at a rates of approximately 105 ring-flips/sec, with an overall energy barrier of 10 kcal/mol (42 kJ/mol), which precludes their separation at ambient temperatures.[17] However, at low temperatures (around –150 °C), the conformer in which the substituent is equatorial crystallizes selectively, and when these crystals are dissolved at very low temperatures, one can directly monitor the approach to equilibrium by NMR spectroscopy as the temperature is raised.[18][19]

The dynamics of conformational (and other kinds of) isomerism can be monitored by NMR spectroscopy at varying temperatures. The technique applies to barriers of 8–14 kcal/mol, and species exhibiting such dynamics are often called "fluxional".

IR spectroscopy is ordinarily used to measure conformer ratios. For the axial and equatorial conformer of bromocyclohexane, νCBr differs by almost 50 cm−1.[17]

Conformation-dependent reactions[edit]

Reaction rates are highly dependent on the conformation of the reactants. This theme is especially well elucidated in organic chemistry. One example is provided by the elimination reactions, which involve the simultaneous removal of a proton and a leaving group from vicinal positions under the influence of a base.

Base-induced bimolecular dehydrohalogenation (an E2 type reaction mechanism). The optimum geometry for the transition state requires the breaking bonds to be antiperiplanar, as they are in the appropriate staggered conformation

The mechanism requires that the departing atoms or groups follow antiparallel trajectories. For open chain substrates this geometric prerequisite is met by at least one of the three staggered conformers. For some cyclic substrates such as cyclohexane, however, an antiparallel arrangement may not be attainable depending on the substituents which might set a conformational lock.[20] Adjacent substituents on a cyclohexane ring can achieve antiperiplanarity only when they occupy trans diaxial positions.

One consequence of this analysis is that trans-4-tert-butylcyclohexyl chloride cannot easily eliminate but instead undergoes substitution (see diagram below) because the most stable conformation has the bulky t-Bu group in the equatorial position, therefore the chloride group is not antiperiplanar with any vicinal hydrogen. The thermodynamically unfavored conformation has the t-Bu group in the axial position, which is higher in energy by (see A value) more than 5 kcal/mol.[21] As a result, the t-Bu group "locks" the ring in the conformation where it is in the equatorial position and substitution reaction is observed. On the other hand, cis-4-tert-butylcyclohexyl chloride undergoes elimination because antiperiplanarity of Cl and H can be achieved when the t-Bu group is in the favorable equatorial position.

Thermodynamically unfavored conformation of trans-4-tert-butylcyclohexyl chloride where the t-Bu group is in the axial position exerting 7-atom interactions.
The trans isomer can attain antiperiplanarity only via the unfavored axial conformer; therefore, it does not eliminate. The cis isomer is already in the correct geometry in its most stable conformation; therefore, it eliminates easily.

These examples notwithstanding, there are many cases in which the dominant product arises from the reaction of the less prevalent conformer, by virtue of the Curtin-Hammett principle. This type of situation can occur whenever conformational equilibration is much faster than reaction to form the product. Thus, it is dangerous to make predictions about the product, based solely on considerations of conformer stability.


See also[edit]

References[edit]

  1. ^ a b c Moss, GP (1996-01-01). "Basic terminology of stereochemistry (IUPAC Recommendations 1996)". Pure and Applied Chemistry. 68 (12): 2193–2222. doi:10.1351/pac199668122193. ISSN 1365-3075.
  2. ^ IUPAC, Compendium of Chemical Terminology, 2nd ed. (the "Gold Book") (1997). Online corrected version:  (1996) "Free rotation (hindered rotation, restricted rotation)". doi:10.1351/goldbook.F02520
  3. ^ Ōki, Michinori (1983) Recent Advances in Atropisomerism, in Topics in Stereochemistry, Vol. 14 (N. L. Allinger, E. L. Eliel and S. H. Wilen, Eds.), Hoboken, NJ:John Wiley & Sons, pp. 1-82; published online in 2007, DOI: 10.1002/9780470147238.ch1, see [1] and [2], accessed 12 June 2014.
  4. ^ Alkorta, Ibon; Jose Elguero; Christian Roussel; Nicolas Vanthuyne; Patrick Piras (2012). Atropisomerism and Axial Chirality in Heteroaromatic Compounds. Advances in Heterocyclic Chemistry. 105. pp. 1–188. doi:10.1016/B978-0-12-396530-1.00001-2. hdl:10261/62060. ISBN 9780123965301.
  5. ^ Hunt, Ian. "Stereochemistry". University of Calgary. Retrieved 28 October 2013.
  6. ^ a b c Anslyn, Eric; Dennis Dougherty (2006). Modern Physical Organic Chemistry. University Science. p. 95. ISBN 978-1891389313.
  7. ^ Barton, Derek. "The Principles of Conformational Analysis". Nobel Media AB 2013. Elsevier Publishing Co. Retrieved 10 November 2013.
  8. ^ J, McMurry (2012). Organic chemistry (8 ed.). Belmont, CA: Brooks/Cole. p. 98. ISBN 9780840054449.
  9. ^ Bauld, Nathan. "Butane Conformational Analysis". University of Texas. Retrieved 28 October 2013.
  10. ^ Bruzik, Karol. "Chapter 6: Conformation". University of Illinois at Chicago. Archived from the original on 11 November 2013. Retrieved 10 November 2013.
  11. ^ The standard enthalpy change ΔH° from gauche to anti is –0.88 kcal/mol. However, because there are two possible gauche forms, there is a statistical factor that needs to be taken into account as an entropic term. Thus, ΔG° = ΔH° – TΔS° = ΔH° + RT ln 2 = –0.88 kcal/mol + 0.41 kcal/mol = –0.47 kcal/mol, at 298 K.
  12. ^ Rzepa, Henry. "Conformational Analysis". Imperial College London. Retrieved 11 November 2013.
  13. ^ Liu, Shubin (7 February 2013). "Origin and Nature of Bond Rotation Barriers: A Unified View". The Journal of Physical Chemistry A. 117 (5): 962–965. Bibcode:2013JPCA..117..962L. doi:10.1021/jp312521z. PMID 23327680.
  14. ^ Carey, Francis A. (2011). Organic chemistry (8th ed.). New York: McGraw-Hill. p. 105. ISBN 978-0-07-340261-1.
  15. ^ McNaught (1997). "Atropisomers". IUPAC Compendium of Chemical Terminology. Oxford: Blackwell Scientific Publications. doi:10.1351/goldbook.A00511. ISBN 978-0967855097.
  16. ^ Dalton, Louisa. "Karplus Equation". Chemical and Engineering News. American Chemical Society. Retrieved 2013-10-27.
  17. ^ a b Eliel, E. L.; Wilen, S. H.; Mander, L. N. (1994). Stereochemistry Of Organic Compounds. J. Wiley and Sons. ISBN 978-0-471-01670-0.
  18. ^ Dunbrack, R. (2002). "Rotamer Libraries in the 21st Century". Current Opinion in Structural Biology. 12 (4): 431–440. doi:10.1016/S0959-440X(02)00344-5. PMID 12163064.
  19. ^ Jensen, Frederick R.; Bushweller, C. Hackett (1969-06-01). "Separation of conformers. II. Axial and equatorial isomers of chlorocyclohexane and trideuteriomethoxycyclohexane". Journal of the American Chemical Society. 91 (12): 3223–3225. doi:10.1021/ja01040a022. ISSN 0002-7863.
  20. ^ "Cycloalkanes". Imperial College London. Retrieved 28 October 2013.
  21. ^ Dougherty, Eric V. Anslyn; Dennis, A. (2006). Modern Physical Organic Chemistry (Dodr. ed.). Sausalito, CA: University Science Books. p. 104. ISBN 978-1-891389-31-3.
Retrieved from "https://en.wikipedia.org/w/index.php?title=Conformational_isomerism&oldid=881971003"