Subderivative

A convex function (blue) and "subtangent lines" at x₀ (red).

In mathematics, the subderivative, subgradient, and subdifferential generalize the derivative to convex functions which are not necessarily differentiable. Subderivatives arise in convex analysis, the study of convex functions, often in connection to convex optimization.

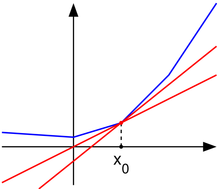
Let f:I→R be a real-valued convex function defined on an open interval of the real line. Such a function need not be differentiable at all points: For example, the absolute value function f(x)=|x| is nondifferentiable when x=0. However, as seen in the graph on the right (where f(x) in blue has non-differentiable kinks similar to the absolute value function), for any x₀ in the domain of the function one can draw a line which goes through the point (x₀, f(x₀)) and which is everywhere either touching or below the graph of f. The slope of such a line is called a subderivative (because the line is under the graph of f).

Definition

Rigorously, a subderivative of a convex function f:I→R at a point x₀ in the open interval I is a real number c such that

$f(x)-f(x_{0})\geq c(x-x_{0})$

for all x in I. One may show that the set of subderivatives at x₀ for a convex function is a nonempty closed interval [a, b], where a and b are the one-sided limits

$a=\lim _{x\to x_{0}^{-}}{\frac {f(x)-f(x_{0})}{x-x_{0}}}$

$b=\lim _{x\to x_{0}^{+}}{\frac {f(x)-f(x_{0})}{x-x_{0}}}$

which are guaranteed to exist and satisfy a ≤ b.

The set [a, b] of all subderivatives is called the subdifferential of the function f at x₀. Since f is convex, if its subdifferential at $x_{0}$ contains exactly one subderivative, then f is differentiable at $x_{0}$.

Examples

Consider the function f(x)=|x| which is convex. Then, the subdifferential at the origin is the interval [−1, 1]. The subdifferential at any point x₀<0 is the singleton set {−1}, while the subdifferential at any point x₀>0 is the singleton set {1}. This is similar to the sign function, but is not a single-valued function at 0, instead including all possible subderivatives.

Properties

• A convex function f:I→R is differentiable at x₀ if and only if the subdifferential is made up of only one point, which is the derivative at x₀.
• A point x₀ is a global minimum of a convex function f if and only if zero is contained in the subdifferential, that is, in the figure above, one may draw a horizontal "subtangent line" to the graph of f at (x₀, f(x₀)). This last property is a generalization of the fact that the derivative of a function differentiable at a local minimum is zero.
• If $f$ and $g$ are convex functions with subdifferentials $\partial f(x)$ and $\partial g(x)$, then the subdifferential of $f+g$ is $\partial (f+g)(x)=\partial f(x)+\partial g(x)$ (where the addition operator denotes the Minkowski sum). This reads as "the subdifferential of a sum is the sum of the subdifferentials."

The subgradient

The concepts of subderivative and subdifferential can be generalized to functions of several variables. If f:U→ R is a real-valued convex function defined on a convex open set in the Euclidean space Rⁿ, a vector $v$ in that space is called a subgradient at a point x₀ in U if for any x in U one has

$f(x)-f(x_{0})\geq v\cdot (x-x_{0})$

where the dot denotes the dot product. The set of all subgradients at x₀ is called the subdifferential at x₀ and is denoted ∂f(x₀). The subdifferential is always a nonempty convex compact set.

These concepts generalize further to convex functions f:U→ R on a convex set in a locally convex space V. A functional $v$^∗ in the dual space V^∗ is called subgradient at x₀ in U if for any x in U

$f(x)-f(x_{0})\geq v^{*}(x-x_{0}).$

The set of all subgradients at x₀ is called the subdifferential at x₀ and is again denoted ∂f(x₀). The subdifferential is always a convex closed set. It can be an empty set; consider for example an unbounded operator, which is convex, but has no subgradient. If f is continuous, the subdifferential is nonempty.

History

The subdifferential on convex functions was introduced by Jean Jacques Moreau and R. Tyrrell Rockafellar in the early 1960s. The generalized subdifferential for nonconvex functions was introduced by F.H. Clarke and R.T. Rockafellar in the early 1980s.

See also

• Weak derivative
• Subgradient method

References

• Jean-Baptiste Hiriart-Urruty, Claude Lemaréchal, Fundamentals of Convex Analysis, Springer, 2001. ISBN 3-540-42205-6.
• Zălinescu, C. (2002). Convex analysis in general vector spaces. World Scientific Publishing  Co., Inc. pp. xx+367. ISBN 981-238-067-1. MR 1921556.