Chomsky hierarchy
In the formal languages of computer science and linguistics, the Chomsky hierarchy is a containment hierarchy of classes of formal grammars. This hierarchy of grammars was described by Noam Chomsky in 1956.[1]
Contents
Formal grammars[edit]
A formal grammar of this type consists of a finite set of production rules (left-hand side → right-hand side), where each side consists of a finite sequence of the following symbols:
- a finite set of nonterminal symbols (indicating that some production rule can yet be applied)
- a finite set of terminal symbols (indicating that no production rule can be applied)
- a start symbol (a distinguished nonterminal symbol)
A formal grammar provides an axiom schema for (or generates) a formal language, which is a (usually infinite) set of finite-length sequences of symbols that may be constructed by applying production rules to another sequence of symbols (which initially contains just the start symbol). A rule may be applied by replacing an occurrence of the symbols on its left-hand side with those that appear on its right-hand side. A sequence of rule applications is called a derivation. Such a grammar defines the formal language: all words consisting solely of terminal symbols which can be reached by a derivation from the start symbol.
Nonterminals are often represented by uppercase letters, terminals by lowercase letters, and the start symbol by S. For example, the grammar with terminals {a, b}, nonterminals {S, A, B}, production rules
- S → AB
- S → ε (where ε is the empty string)
- A → aS
- B → b
and start symbol S, defines the language of all words of the form (i.e. n copies of a followed by n copies of b).
The following is a simpler grammar that defines the same language: Terminals {a, b}, Nonterminals {S}, Start symbol S, Production rules
- S → aSb
- S → ε
As another example, a grammar for a toy subset of English language is given by:
- terminals
- {generate, hate, great, green, ideas, linguists}
- nonterminals
- {SENTENCE, NOUNPHRASE, VERBPHRASE, NOUN, VERB, ADJ}
- production rules
- SENTENCE → NOUNPHRASE VERBPHRASE
- NOUNPHRASE → ADJ NOUNPHRASE
- NOUNPHRASE → NOUN
- VERBPHRASE → VERB NOUNPHRASE
- VERBPHRASE → VERB
- NOUN → ideas
- NOUN → linguists
- VERB → generate
- VERB → hate
- ADJ → great
- ADJ → green
and start symbol SENTENCE. An example derivation is
- SENTENCE → NOUNPHRASE VERBPHRASE → ADJ NOUNPHRASE VERBPHRASE → ADJ NOUN VERBPHRASE → ADJ NOUN VERB NOUNPHRASE → ADJ NOUN VERB ADJ NOUNPHRASE → ADJ NOUN VERB ADJ ADJ NOUNPHRASE → ADJ NOUN VERB ADJ ADJ NOUN → great NOUN VERB ADJ ADJ NOUN → great linguists VERB ADJ ADJ NOUN → great linguists generate ADJ ADJ NOUN → great linguists generate great ADJ NOUN → great linguists generate great green NOUN → great linguists generate great green ideas.
Other sequences that can be derived from this grammar are: "ideas hate great linguists", and "ideas generate". While these sentences are nonsensical, they are syntactically correct. A syntactically incorrect sentence ( e.g. "ideas ideas great hate") cannot be derived from this grammar. See "Colorless green ideas sleep furiously" for a similar example given by Chomsky in 1957; see Phrase structure grammar and Phrase structure rules for more natural language examples and the problems of formal grammar in that area.
The hierarchy[edit]
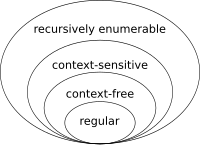
The following table summarizes each of Chomsky's four types of grammars, the class of language it generates, the type of automaton that recognizes it, and the form its rules must have.
| Grammar | Languages | Automaton | Production rules (constraints)* | Examples[2] |
|---|---|---|---|---|
| Type-0 | Recursively enumerable | Turing machine | (where contains at least one non-terminal) | describes a terminating Turing machine |
| Type-1 | Context-sensitive | Linear-bounded non-deterministic Turing machine | ||
| Type-2 | Context-free | Non-deterministic pushdown automaton | ||
| Type-3 | Regular | Finite state automaton | and |
|
* Meaning of symbols:
| ||||
Note that the set of grammars corresponding to recursive languages is not a member of this hierarchy; these would be properly between Type-0 and Type-1.
Every regular language is context-free, every context-free language is context-sensitive, every context-sensitive language is recursive and every recursive language is recursively enumerable. These are all proper inclusions, meaning that there exist recursively enumerable languages that are not context-sensitive, context-sensitive languages that are not context-free and context-free languages that are not regular.
Type-0 grammars[edit]
Type-0 grammars include all formal grammars. They generate exactly all languages that can be recognized by a Turing machine. These languages are also known as the recursively enumerable or Turing-recognizable languages.[3] Note that this is different from the recursive languages, which can be decided by an always-halting Turing machine.
Type-1 grammars[edit]
Type-1 grammars generate context-sensitive languages. These grammars have rules of the form with a nonterminal and , and strings of terminals and/or nonterminals. The strings and may be empty, but must be nonempty. The rule is allowed if does not appear on the right side of any rule. The languages described by these grammars are exactly all languages that can be recognized by a linear bounded automaton (a nondeterministic Turing machine whose tape is bounded by a constant times the length of the input.)
Type-2 grammars[edit]
Type-2 grammars generate the context-free languages. These are defined by rules of the form with being a nonterminal and being a string of terminals and/or nonterminals. These languages are exactly all languages that can be recognized by a non-deterministic pushdown automaton. Context-free languages—or rather its subset of deterministic context-free language—are the theoretical basis for the phrase structure of most programming languages, though their syntax also includes context-sensitive name resolution due to declarations and scope. Often a subset of grammars is used to make parsing easier, such as by an LL parser.
Type-3 grammars[edit]
Type-3 grammars generate the regular languages. Such a grammar restricts its rules to a single nonterminal on the left-hand side and a right-hand side consisting of a single terminal, possibly followed by a single nonterminal (right regular). Alternatively, the right-hand side of the grammar can consist of a single terminal, possibly preceded by a single nonterminal (left regular). These generate the same languages. However, if left-regular rules and right-regular rules are combined, the language need no longer be regular. The rule is also allowed here if does not appear on the right side of any rule. These languages are exactly all languages that can be decided by a finite state automaton. Additionally, this family of formal languages can be obtained by regular expressions. Regular languages are commonly used to define search patterns and the lexical structure of programming languages.
References[edit]
- ^ Chomsky, Noam (1956). "Three models for the description of language" (PDF). IRE Transactions on Information Theory (2): 113–124. doi:10.1109/TIT.1956.1056813.
- ^ http://www.cs.ru.nl/~herman/onderwijs/2016TnA/lecture7.pdf
- ^ Michael Sipser (1997). Introduction to the Theory of Computation 1st. Cengage Learning. ISBN 0-534-94728-X.
The Church-Turing Thesis (Page 130)
- Chomsky, Noam (1959). "On certain formal properties of grammars" (PDF). Information and Control. 2 (2): 137–167. doi:10.1016/S0019-9958(59)90362-6.
- Chomsky, Noam; Schützenberger, Marcel P. (1963). "The algebraic theory of context free languages". In Braffort, P.; Hirschberg, D. Computer Programming and Formal Languages (PDF). Amsterdam: North Holland. pp. 118–161.
- Davis, Martin D.; Sigal, Ron; Weyuker, Elaine J. (1994). Computability, Complexity, and Languages: Fundamentals of Theoretical Computer Science (2nd ed.). Boston: Academic Press, Harcourt, Brace. p. 327. ISBN 0-12-206382-1.