Monad (category theory)

Not to be confused with Monad (linear algebra).

For the uses of monads in computer software, see monads in functional programming.

In category theory, a branch of mathematics, a monad (also triple, triad, standard construction and fundamental construction) is an endofunctor (a functor mapping a category to itself), together with two natural transformations. Monads are used in the theory of pairs of adjoint functors, and they generalize closure operators on partially ordered sets to arbitrary categories.

Overview

A monad is a certain type of endofunctor. For example, if $F$ and $G$ are a pair of adjoint functors, with $F$ left adjoint to $G$, then the composition $G\circ F$ is a monad. If $F$ and $G$ are inverse functors, the corresponding monad is the identity functor. In general, adjunctions are not equivalences—they relate categories of different natures. The monad theory matters as part of the effort to capture what it is that adjunctions 'preserve'. The other half of the theory, of what can be learned likewise from consideration of $F\circ G$, is discussed under the dual theory of comonads.

The monad axioms can be seen at work in this example: let $G$ be the forgetful functor from the category Grp of groups to the category Set of sets, and let $F$ be the free group functor from the category of sets to the category of groups. Then $F$ is left adjoint of $G$.

The monad

$T=G\circ F$

takes a set $X$ and returns the underlying set of the free group $\mathrm {Free} (X)$. In this situation, we are given two natural morphisms:

$X\rightarrow T(X)$

by including any set $X$ into the set $\mathrm {Free} (X)$ in the natural way, as strings of length 1. Further,

$T(T(X))\rightarrow T(X)$

can be made out of a natural concatenation or 'flattening' of 'strings of strings'. This amounts to two natural transformations

$I\rightarrow T$

and

$T\circ T\rightarrow T{\text{.}}$

They will satisfy some axioms about identity and associativity that result from the adjunction properties. These are the monad axioms.

Another example is when $T$ is the endofunctor on the category of vector spaces which maps a vector space $V$ to its tensor algebra $T(V)$, and which maps linear maps to their tensor product. We then have a natural transformation corresponding to the embedding of $V$ into its tensor algebra, and a natural transformation corresponding to the map from $T(T(V))$ to $T(V)$ obtained by simply expanding all tensor products. These satisfy the monad axioms.

Those axioms are formally similar to the monoid axioms. They are taken as the definition of a general monad (not assumed a priori to be connected to an adjunction) on a category.

If we specialize to categories arising from partially ordered sets $(P,\leq )$ (with a single morphism from $x$ to $y$ iff $x\leq y$), then the formalism becomes much simpler: adjoint pairs are Galois connections and monads are closure operators.

Every monad arises from some adjunction, in fact typically from many adjunctions. Two constructions introduced below, the Kleisli category and the category of Eilenberg–Moore algebras, are extremal solutions to the problem of constructing an adjunction that gives rise to a given monad.

The example about free groups given above can be generalized to any type of algebra in the sense of a variety of algebras in universal algebra. Thus, every such type of algebra gives rise to a monad on the category of sets. Importantly, the algebra type can be recovered from the monad (as the category of Eilenberg–Moore algebras), so monads can also be seen as generalizing varieties of universal algebras. Even more generally, any adjunction is said to be monadic (or tripleable) if it shares this property of being (equivalent to) the Eilenberg–Moore category of its associated monad. Consequently, Beck's monadicity theorem, which gives a criterion for monadicity, can be used to show that an arbitrary adjunction can be treated as a category of algebras in this way.

The notion of monad was invented by Roger Godement in 1958 under the name "standard construction." In the 1960s and 1970s, many people used the name "triple." The now standard term "monad" is due to Saunders Mac Lane.

Formal definition

If $C$ is a category, a monad on $C$ consists of an endofunctor $T\colon C\to C$ together with two natural transformations: $\eta \colon 1_{C}\to T$ (where $1_{C}$ denotes the identity functor on $C$) and $\mu \colon T^{2}\to T$ (where $T^{2}$ is the functor $T\circ T$ from $C$ to $C$). These are required to fulfill the following conditions (sometimes called coherence conditions):

• $\mu \circ T\mu =\mu \circ \mu T$ (as natural transformations $T^{3}\to T$);
• $\mu \circ T\eta =\mu \circ \eta T=1_{T}$ (as natural transformations $T\to T$; here $1_{T}$ denotes the identity transformation from $T$ to $T$).

We can rewrite these conditions using the following commutative diagrams:

See the article on natural transformations for the explanation of the notations $T\mu$ and $\mu T$, or see below the commutative diagrams not using these notions:

The first axiom is akin to the associativity in monoids if we think of $\mu$ as the monoid's binary operation, and the second axiom is akin to the existence of an identity element (which we think of as given by $\eta$). Indeed, a monad on $C$ can alternatively be defined as a monoid in the category $\mathbf {End} _{C}$ whose objects are the endofunctors of $C$ and whose morphisms are the natural transformations between them, with the monoidal structure induced by the composition of endofunctors.

Examples

A rich set of examples is given by adjunctions (see Monads and adjunctions, below), and the free group example mentioned above belongs to that set.

Here is another example, on the category $\mathbf {Set}$: For a set $A$ let $T(A)$ be the power set of $A$ and for a function $f\colon A\to B$ let $T(f)$ be the function between the power sets induced by taking direct images under $f$. For every set $A$, we have a map $\eta _{A}\colon A\to T(A)$, which assigns to every $a\in A$ the singleton $\{a\}$. The function

$\mu _{A}\colon T(T(A))\to T(A)$

takes a set of sets to its union. These data describe a monad.

Closure operators are monads on preorder categories.

Algebras for a monad

See also: F-algebra

Suppose that $(T,\eta ,\mu )$ is a given monad on a category $C$.

A $T$-algebra $(x,h)$ is an object $x$ of $C$ together with an arrow $h\colon Tx\to x$ of $C$ called the structure map of the algebra such that the diagrams

and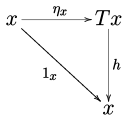

commute.

A morphism $f\colon (x,h)\to (x',h')$ of $T$-algebras is an arrow $f\colon x\to x'$ of $C$ such that the diagram

commutes.

The category $C^{T}$ of $T$-algebras and their morphisms is called the Eilenberg–Moore category or category of (Eilenberg–Moore) algebras of the monad $T$. The forgetful functor $C^{T}$→$C$ has a left adjoint $C$→$C^{T}$ taking $x$ to the free algebra $(Tx,\mu _{x})$.

Given the monad $T$, there exists another "canonical" category $C_{T}$ called the Kleisli category of the monad $T$. This category is equivalent to the category of free algebras for the monad $T$, i. e. the full subcategory of $C^{T}$ whose objects are of the form $(Tx,\mu _{x})$, for $x$ an object of $C$.

Monads and adjunctions

An adjunction $(F,G,\eta ,\varepsilon )$ between two categories $C$ and $D$ (where $F\colon C\to D$ is left adjoint to $G\colon D\to C$ and $\eta$ and $\varepsilon$ are respectively the unit and the counit) always defines a monad $(GF,\eta ,G\varepsilon F)$.

Conversely, it is interesting to consider the adjunctions which define a given monad $(T,\eta ,\mu )$ this way. Let $\mathbf {Adj} (C,T)$ be the category whose objects are the adjunctions $(F,G,e,\varepsilon )$ such that $(GF,e,G\varepsilon F)=(T,\eta ,\mu )$ and whose arrows are the morphisms of adjunctions which are the identity on $C$. Then this category has

• an initial object $(F_{T},G_{T},\eta ,\mu _{T}):C\to C_{T}$, where $C_{T}$ is the Kleisli category,
• a terminal object $(F^{T},G^{T},\eta ,\mu ^{T}):C\to C^{T}$, where $C^{T}$ is the Eilenberg–Moore category.

An adjunction $(F,G,\eta ,\varepsilon )$ between two categories $C$ and $D$ is a monadic adjunction when the category $D$ is equivalent to the Eilenberg–Moore category $C^{T}$ for the monad $T=GF$. (Mac Lane uses a stronger definition, where the two categories are isomorphic rather than equivalent.) By extension, a functor $G\colon D\to C$ is said to be monadic if it has a left adjoint $F$ forming a monadic adjunction. Beck's monadicity theorem gives a characterization of monadic functors.

Comonads and their importance

The categorical dual definition is a formal definition of a comonad (or cotriple); this can be said quickly in the terms that a comonad for a category $C$ is a monad for the opposite category $C^{\mathrm {op} }$. It is therefore a functor $U$ from $C$ to itself, with a set of axioms for counit and comultiplication that come from reversing the arrows everywhere in the definition just given.

Monads are to monoids as comonads are to comonoids. Every set is a comonoid in a unique way, so comonoids are less familiar in in abstract algebra than monoids; however, comonoids in the category of vector spaces with its usual tensor product are important and widely studied under the name of coalgebras.

The importance of comonads becomes visible in a class of theorems from the categorical (and algebraic geometry) theory of descent. What was realised in the period 1960 to 1970 is that recognising the categories of coalgebras for a comonad was an important tool of category theory (particularly topos theory). The results involved are based on Beck's theorem. Roughly what goes on is this: while it is simple set theory that a surjective mapping of sets is as good as the equivalence relation "x is in the same fiber as y" on the domain of the mapping, for geometric morphisms what you should do is pass to such a coalgebra subcategory.

Uses

Monads are used in functional programming to express types of sequential computation (sometimes with side-effects). See monads in functional programming, and the more mathematically oriented Wikibook module b:Haskell/Category theory.

In categorical logic, an analogy has been drawn between the monad-comonad theory, and modal logic via closure operators, interior algebras, and their relation to models of S4 and intuitionistic logics.

Generalization

It is possible to define monads in a 2-category $C$. Monads described above are monads for $C=\mathbf {Cat}$.

See also

• Distributive law between monads
• Lawvere theory
• Monad (functional programming)
• Polyad
• Strong monad

Further reading

• Daniele Turi, Category Theory Lecture Notes (1996–2001), based on Mac Lane's book "Categories for the Working Mathematician".
• Michael Barr and Charles Wells, Category Theory for Computing Science (1999).
• Roger Godement, Topologie Algébrique et Théorie des Faisceaux. Actualités Sci. Ind. No. 1252. Publ. Math. Univ. Strasbourg. No. 13 Hermann, Paris 1958, viii+283 pp.
• Pedicchio, Maria Cristina; Tholen, Walter, eds. (2004). Categorical Foundations. Special Topics in Order, Topology, Algebra, and Sheaf Theory. Encyclopedia of Mathematics and Its Applications. 97. Cambridge: Cambridge University Press. ISBN 0-521-83414-7. Zbl 1034.18001.

External links

• Monads, five short lectures (with one appendix).
• John Baez's This Week's Finds in Mathematical Physics (Week 89) covers monads in 2-categories.