Chunking (psychology)

From Wikipedia, the free encyclopedia
Jump to navigation Jump to search
This article is about chunking as a memory task. For chunking as a method for solving division, see Chunking (division).

In cognitive psychology, chunking is a process by which individual pieces of information are bound together into a meaningful whole (Neath & Surprenant, 2003). A chunk is defined as a familiar collection of more elementary units that have been inter-associated and stored in memory repeatedly and act as a coherent, integrated group when retrieved (Tulving & Craik, 2000).

It is believed that individuals create higher order cognitive representations of the items on the list that are more easily remembered as a group than as individual items themselves. Representations of these groupings are highly subjective, as they depend critically on the individual's perception of the features of the items and the individual's semantic network. The size of the chunks generally ranges anywhere from two to six items, but differs based on language and culture.

The phenomenon of chunking as a memory mechanism can be observed in the way individuals group numbers and information in the day-to-day life. For example, when recalling a number such as 12101946, if numbers are grouped as 12, 10 and 1946, a mnemonic is created for this number as a day, month and year. Similarly, another illustration of the limited capacity of working memory as suggested by George Miller can be seen from the following example: While recalling a mobile phone number such as 9849523450, we might break this into 98 495 234 50. Thus, instead of remembering 10 separate digits that is beyond the "seven plus-or-minus two" memory span, we are remembering four groups of numbers.

A modality effect is present in chunking. That is, the mechanism used to convey the list of items to the individual affects how much "chunking" occurs. Experimentally, it has been found that auditory presentation results in a larger amount of grouping in the responses of individuals, as compared to visual presentation. Previous literature, such as George Miller's The Magical Number Seven, Plus or Minus Two: Some Limits on our Capacity for Processing Information (1956) have shown that the probability of recall is greater when the "chunking" strategy is used. As stated above, the grouping of the responses occurs as individuals place them into categories according to their inter-relatedness based on semantic and perceptual properties. Lindley (1966) showed that the groups produced have meaning to the participant, therefore; this strategy makes it easier for an individual to recall and maintain information in memory during studies and testing. Therefore, when "chunking" is used as a strategy, one can expect a higher proportion of correct recalls.

Various kinds of memory training systems and mnemonics include training and drill in specially-designed recoding or chunking schemes. Such systems existed before Miller's paper, but there was no convenient term to describe the general strategy or substantive and reliable research. The term "chunking" is now often used in reference to these systems. As an illustration, patients with Alzheimer's disease typically experience working memory deficits; chunking is an effective method to improve patients' verbal working memory performance (Huntley, Bor, Hampshire, Owen, & Howard, 2011). Another classic example of chunking is discussed in the "Expertise and skilled memory effects" section below.

"Magic number seven"[edit]

Main article: The Magical Number Seven, Plus or Minus Two

The word chunking comes from a famous 1956 paper by George A. Miller, "The Magical Number Seven, Plus or Minus Two: Some Limits on Our Capacity for Processing Information" (Neisser, 1967). At a time when information theory was beginning to be applied in psychology, Miller observed that some human cognitive tasks fit the model of a "channel capacity" characterized by a roughly constant capacity in bits, but short-term memory did not. A variety of studies could be summarized by saying that short-term memory had a capacity of about "seven plus-or-minus two" chunks. Miller (1956) wrote, "With binary items the span is about nine and, although it drops to about five with monosyllabic English words, the difference is far less than the hypothesis of constant information would require (see also, memory span). The span of immediate memory seems to be almost independent of the number of bits per chunk, at least over the range that has been examined to date." Miller acknowledged that "we are not very definite about what constitutes a chunk of information"

Miller (1956) noted that according to this theory, it should be possible to increase short-term memory for low-information-content items effectively by mentally recoding them into a smaller number of high-information-content items. "A man just beginning to learn radio-telegraphic code hears each dit and dah as a separate chunk. Soon he is able to organize these sounds into letters and then he can deal with the letters as chunks. Then the letters organize themselves as words, which are still larger chunks, and he begins to hear whole phrases." Thus, a telegrapher can effectively "remember" several dozen dits and dahs as a single phrase. Naive subjects can remember about only nine binary items, but Miller reports a 1954 experiment in which people were trained to listen to a string of binary digits and (in one case) mentally group them into groups of five, recode each group into a name (for example, "twenty-one" for 10101), and remember the names. With sufficient drill, people found it possible to remember as many as forty binary digits. Miller wrote:

It is a little dramatic to watch a person get 40 binary digits in a row and then repeat them back without error. However, if you think of this merely as a mnemonic trick for extending the memory span, you will miss the more important point that is implicit in nearly all such mnemonic devices. The point is that recoding is an extremely powerful weapon for increasing the amount of information that we can deal with.

Expertise and skilled memory effects[edit]

Studies have shown that people have better memories when they are trying to remember items with which they are familiar. Similarly, people tend to create chunks with which they are familiar. This familiarity allows them to remember more individual pieces of content, and also more chunks as a whole. One well-known chunking study was conducted by Chase and Ericsson, who worked with an undergraduate student, SF, over two years. Chase and Ericsson wanted to see if a person's digit span could be improved with practice. SF began the experiment with a normal span of 7 digits. SF was a long-distance runner, and chunking strings of digits into race times increased his digit span. By the end of the experiment his digit span had grown to 80 numbers. The book The Brain-Targeted Teaching Model for 21st Century Schools (2012) states that SF later expanded his strategy by incorporating ages and years, but his chunks were always familiar, and thus allowed him to recall the to-be-remembered chunks more easily. It is important to note that a person who does not have knowledge in the expert domain (e.g. being familiar with mile/marathon times) would have difficulty chunking with race times and ultimately be unable to memorize as many numbers using this method.

Chunking in motor learning[edit]

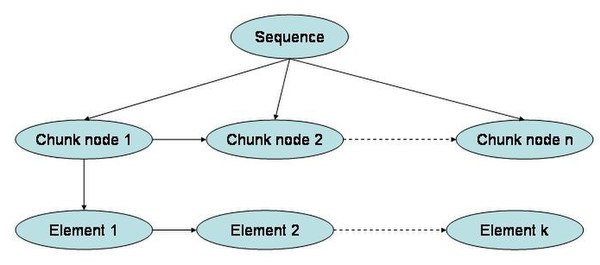
Chunking is a flexible way of learning. Karl Lashley, in his classic paper on serial order (Lashley, 1951), argued that the sequential responses that appear to be organized in a linear and flat fashion concealed an underlying hierarchical structure. This was demonstrated in motor control by Rosenbaum et al. (1983). Thus sequences can consist of sub-sequences and these can in turn consist of sub-sub-sequences. Hierarchical representations of sequences have an edge over linear representations. They combine efficient local action at low hierarchical levels while maintaining the guidance of an overall structure. While the representation of a linear sequence is simple from storage point of view, there can be potential problems during retrieval. For instance, if there is a break in the sequence chain, subsequent elements will become inaccessible. On the other hand, a hierarchical representation would have multiple levels of representation. A break in the link between lower level nodes does not render any part of the sequence inaccessible, since the control nodes (chunk nodes) at the higher level would still be able to facilitate access to the lower level nodes.

Schematic of a hierarchical sequential structure with three levels. The lowest level could be a linear representation, while intermediate levels denote chunk nodes. The highest level is the entire sequence.

Chunks in motor learning are identified by pauses between successive actions (Terrace, 2001). He also suggested that during the sequence performance stage (after learning), participants download list items as chunks during pauses. Terrace also argued for an operational definition of chunks suggesting a distinction between the notions of input and output chunks from the ideas of short-term and long-term memory. Input chunks reflect the limitation of working memory during the encoding of new information (how new information is stored in long-term memory), and how it is retrieved during subsequent recall. Output chunks reflect the organization of over-learned motor programs that are generated on-line in working memory. Sakai et al. (2003) showed that participants spontaneously organize a sequence into a number of chunks across few sets, and that these chunks were distinct among participants tested on the same sequence. Sakai et al. (2003) showed that performance of a shuffled sequence was poorer when the chunk patterns were disrupted than when the chunk patterns were preserved. Chunking patterns also seem to depend on the effectors used.

Chunking as the learning of long-term memory structures[edit]

This usage derives from Miller's (1956) idea of chunking as grouping, but the emphasis is now on long-term memory rather than only on short-term memory. A chunk can then be defined as "a collection of elements having strong associations with one another, but weak associations with elements within other chunks" (Gobet et al., 2001, p. 236). Chase and Simon (1973) and later Gobet, Retschitzki and de Voogt (2004) showed that chunking could explain several phenomena linked to expertise in chess. To be more specific, more skilled chess players have a larger chunk size. Several successful computational models of learning and expertise have been developed using this idea, such as EPAM (Elementary Perceiver and Memorizer) and CHREST (Chunk Hierarchy and REtrieval STructures). Chunking has also been used with models of language acquisition (Barnard, Lieven, & Tomasello, 2009).

See also[edit]

References[edit]

Further reading[edit]

External links[edit]

Retrieved from "https://en.wikipedia.org/w/index.php?title=Chunking_(psychology)&oldid=882582503"