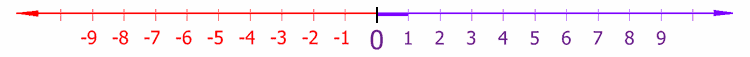Számegyenes
A számegyenes a matematika területéhez tartozó fogalom, a valós számok halmazának reprezentálására használt grafikai eszköz. Bevezetése John Wallis angol matematikus nevéhez kötődik.
Megjelenése egy végtelen hosszúságú egyenes vonal. A vonal folytonos, azaz bármilyen erős nagyításban is nézzük, sosem láthatunk rajta szakadási helyet. Az egyenes minden geometriai pontja egy valós számot ábrázol. A számegyenes értelmezhetőségének feltétele, hogy rajta legalább két számhoz tartozó pont ismert (megjelölt) legyen, ezáltal lesz az egyenes kalibrálva, ennek ismeretében lehet más számokat jelölő pontok helyét kijelölni. A számegyenesen bármelyik két szám különbsége mindig egyenesen arányos a két számot jelölő pontok geometriai távolságával, egyszerűbben: a számegyenesen a számok egyenletesen helyezkednek el, hacsak az ettől a szabálytól való eltérés nincs külön megjelölve.
A végtelen hosszú számegyenesnek a gyakorlatban csak egy szakaszát tudjuk megjeleníteni. A hagyományos ábrázolás szerint vízszintesen rajzolt egyenesen jobbra haladva növekszik a számok értéke, ezt nevezzük pozitív iránynak, balra a számok értéke csökken, ez a negatív irány. Az egyenes irányítottsága a rajta megjelölt legalább két szám alapján egyértelműen adódik. A végtelen hosszúságra való emlékeztetőül szokás az egyenes szakasz mindkét végét nyíllal lezárni, egy másik szokás szerint csak az egyenes pozitív irányú végére teszünk egy nyílfejet.
A számegyenesnek van két kitüntetett pontja. Az egyik az origó,[1] amely a nulla számnak a helyét jelöli, a másik az 1 helye. A két pont közötti geometriai és algebrai távolság az egység. Nem kötelező, hogy ezek a pontok láthatóak legyenek a számegyenes egy adott rajzán, ha a rajzon legalább két pont által ábrázolt számérték ismert.
Az egyenesen végtelen hosszúságban, egyenletes közökben sorakoznak az egész számokat ábrázoló pontok. Ezeket a véges közönséges törtek alakjában felírható egyéb számok kiegészítik a racionális számok halmazává. A racionális számoknak a számegyenesen megfelelő pontok végtelen sűrűségben, mégis egymástól elkülönülően találhatók. Vagyis a racionális számok pontjai között mindig végtelen sok irracionális szám áll, de nem tudjuk a számegyenest olyan nagyításban megnézni, amelyben a racionális számok már láthatóan elkülönülnének. A racionális és irracionális számok diszjunkt halmazainak unióját nevezzük valós számoknak, ezek már összefüggő egyenest alkotnak. Ez azt jelenti, hogy a számegyenes bármilyen nagyításban is nézett bármelyik pontjához tartozik pontosan egy valós szám, illetve bármelyik valós szám helye megtalálható a számegyenes pontjainak egyikén. (Az egyenes alkalmassága valós számok különbségének kifejezésére annyira kézenfekvő, hogy a Birkhoff-féle vonalzó-axióma alakjában egy teljes geometriai rendszer egyik alappillére lett.)
A számegyenest gyakran használják az összeadás és a kivonás tanítására, mivel két szám algebrai különbsége mindig arányos a két számnak megfelelő pontok közötti geometriai távolsággal, tehát a műveletek egyszerűen szemléltethetőek. Ilyenkor fel szokás tüntetni az egész számoknak megfeleltethető pontok helyét, mert ez a kisiskolások számára megkönnyíti a mértékek számlálását, de ilyen skála készítése egyébként nem kötelező.
Azt a tényt, hogy a logaritmus művelete a számok szorzását logaritmusaik összeadásává transzformálja, az előbbiek nyomán egyszerűen hasznosítja a szorzásra és osztásra régebben sokfelé használt számolóeszköz, a logarléc.
Jegyzetek[szerkesztés]
- ↑ origo = 'eredet' (latin)