Amplitude amplification is a technique in quantum computing which generalizes the idea behind
the Grover's search algorithm, and gives rise to a family of
quantum algorithms.
It was discovered by Gilles Brassard and
Peter Høyer in 1997,[1]
and independently rediscovered by Lov Grover in 1998.[2]
In a quantum computer, amplitude amplification can be used to obtain a
quadratic speedup over several classical algorithms.
Algorithm[edit]
The derivation presented here roughly follows the one given in
.[3]
Assume we have an N-dimensional Hilbert space  representing the state space of our quantum system, spanned by the
orthonormal computational basis states
representing the state space of our quantum system, spanned by the
orthonormal computational basis states  .
Furthermore assume we have a Hermitian projection operator
.
Furthermore assume we have a Hermitian projection operator  .
Alternatively,
.
Alternatively,  may be given in terms of a
Boolean oracle function
may be given in terms of a
Boolean oracle function
 and an orthonormal operational basis
and an orthonormal operational basis
 ,
in which case
,
in which case
 .
.
 can be used to partition
can be used to partition
 into a direct sum of two mutually orthogonal subspaces,
the good subspace
into a direct sum of two mutually orthogonal subspaces,
the good subspace  and
the bad subspace
and
the bad subspace  :
:

In other words, we are defining a "
good subspace"

via the projector

. The goal of the algorithm is then to evolve some initial state

into a state belonging to

.
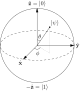
Given a normalized state vector  with nonzero overlap with both subspaces, we can uniquely decompose it as
with nonzero overlap with both subspaces, we can uniquely decompose it as
 ,
,
where ![\theta =\arcsin \left(\left|P|\psi \rangle \right|\right)\in [0,\pi /2]](https://wikimedia.org/api/rest_v1/media/math/render/svg/44ec776775f0b19cdb4f667105947d6e2271a7f6) ,
and
,
and
 and
and  are the
normalized projections of
are the
normalized projections of  into the
subspaces
into the
subspaces  and
and  ,
respectively.
This decomposition defines a two-dimensional subspace
,
respectively.
This decomposition defines a two-dimensional subspace
 , spanned by the vectors
, spanned by the vectors
 and
and  .
The probability of finding the system in a good state when measured
is
.
The probability of finding the system in a good state when measured
is  .
.
Define a unitary operator
 ,
where
,
where

 flips the phase of the states in the good subspace, whereas
flips the phase of the states in the good subspace, whereas
 flips the phase of the initial state
flips the phase of the initial state  .
.
The action of this operator on  is given by
is given by
 and
and .
.
Thus in the  subspace
subspace  corresponds to a rotation by the angle
corresponds to a rotation by the angle  :
:
 .
.
Applying 
 times on the state
times on the state
 gives
gives
 ,
,
rotating the state between the good and bad subspaces.
After  iterations the probability of finding the
system in a good state is
iterations the probability of finding the
system in a good state is  .
.
The probability is maximized if we choose
 .
.
Up until this point each iteration increases the amplitude of the good states, hence
the name of the technique.
Applications[edit]
Assume we have an unsorted database with N elements, and an oracle function
 which can recognize the good entries we are searching for, and
which can recognize the good entries we are searching for, and  for simplicity.
for simplicity.
If there are  good entries in the database in total, then we can find them by
initializing the quantum computer into a uniform superposition
good entries in the database in total, then we can find them by
initializing the quantum computer into a uniform superposition

of all the database elements,
and running the above algorithm. In this case the overlap of the initial state with the good subspace is equal to the
square root of the frequency of the good entries in the database,  .
If
.
If  , we can approximate the number of required iterations as
, we can approximate the number of required iterations as

Measuring the state will now give one of the good entries with a high probability. Since each application of  requires a single oracle query (assuming that the oracle is implemented as a quantum gate),
we can find a good entry with just
requires a single oracle query (assuming that the oracle is implemented as a quantum gate),
we can find a good entry with just  oracle queries, thus obtaining a quadratic speedup over the best possible classical algorithm.
oracle queries, thus obtaining a quadratic speedup over the best possible classical algorithm.
If we set  to one, the above scenario essentially reduces to the original Grover search.
to one, the above scenario essentially reduces to the original Grover search.
References[edit]












![\theta =\arcsin \left(\left|P|\psi \rangle \right|\right)\in [0,\pi /2]](https://wikimedia.org/api/rest_v1/media/math/render/svg/44ec776775f0b19cdb4f667105947d6e2271a7f6)