Deterministic finite automaton

"DFSA" redirects here. DFSA may also refer to drug-facilitated sexual assault.

An example of a deterministic finite automaton that accepts only binary numbers that are multiples of 3. The state S₀ is both the start state and an accept state.

In the theory of computation, a branch of theoretical computer science, a deterministic finite automaton (DFA)—also known as deterministic finite acceptor (DFA), deterministic finite state machine (DFSM), or deterministic finite state automaton (DFSA)—is a finite-state machine that accepts or rejects strings of symbols and only produces a unique computation (or run) of the automaton for each input string. Deterministic refers to the uniqueness of the computation. In search of the simplest models to capture finite-state machines, Warren McCulloch and Walter Pitts were among the first researchers to introduce a concept similar to finite automata in 1943.

The figure illustrates a deterministic finite automaton using a state diagram. In this example automaton, there are three states: S₀, S₁, and S₂ (denoted graphically by circles). The automaton takes a finite sequence of 0s and 1s as input. For each state, there is a transition arrow leading out to a next state for both 0 and 1. Upon reading a symbol, a DFA jumps deterministically from one state to another by following the transition arrow. For example, if the automaton is currently in state S₀ and the current input symbol is 1, then it deterministically jumps to state S₁. A DFA has a start state (denoted graphically by an arrow coming in from nowhere) where computations begin, and a set of accept states (denoted graphically by a double circle) which help define when a computation is successful.

A DFA is defined as an abstract mathematical concept, but is often implemented in hardware and software for solving various specific problems. For example, a DFA can model software that decides whether or not online user input such as email addresses are valid.

DFAs recognize exactly the set of regular languages, which are, among other things, useful for doing lexical analysis and pattern matching. DFAs can be built from nondeterministic finite automata (NFAs) using the powerset construction method.

Formal definition

A deterministic finite automaton $M$ is a 5-tuple, $(Q,\Sigma ,\delta ,q_{0},F)$, consisting of

• a finite set of states $Q$
• a finite set of input symbols called the alphabet $\Sigma$
• a transition function $\delta :Q\times \Sigma \rightarrow Q$
• an initial or start state $q_{0}\in Q$
• a set of accept states $F\subseteq Q$

Let $w=a_{1}a_{2}...a_{n}$ be a string over the alphabet $\Sigma$. The automaton $M$ accepts the string $w$ if a sequence of states, $r_{0},r_{1},...,r_{n}$, exists in $Q$ with the following conditions:

1. $r_{0}=q_{0}$
2. $r_{i+1}=\delta (r_{i},a_{i+1})$, for $i=0,...,n-1$
3. $r_{n}\in F$.

In words, the first condition says that the machine starts in the start state $q_{0}$. The second condition says that given each character of string $w$, the machine will transition from state to state according to the transition function $\delta$. The last condition says that the machine accepts $w$ if the last input of $w$ causes the machine to halt in one of the accepting states. Otherwise, it is said that the automaton rejects the string. The set of strings that $M$ accepts is the language recognized by $M$ and this language is denoted by $L(M)$.

A deterministic finite automaton without accept states and without a starting state is known as a transition system or semiautomaton.

For more comprehensive introduction of the formal definition see automata theory.

Complete and incomplete

According to the above definition, deterministic finite automata are always complete: they define a transition for each state and each input symbol.

While this is the most common definition, some authors use the term deterministic finite automaton for a slightly different notion: an automaton that defines at most one transition for each state and each input symbol; the transition function is allowed to be partial. When no transition is defined, such an automaton halts.

Example

The following example is of a DFA $M$, with a binary alphabet, which requires that the input contains an even number of 0s.

The state diagram for M

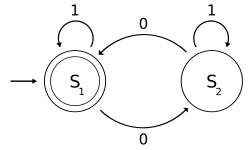
$M=(Q,\Sigma ,\delta ,q_{0},F)$ where

• $Q=\{S_{1},S_{2}\}$
• $\Sigma =\{0,1\}$
• $q_{0}=S_{1}$
• $F=\{S_{1}\}$ and
• $\delta$ is defined by the following state transition table:

	0	1
S1	S2	S1
S2	S1	S2

The state $S_{1}$ represents that there has been an even number of 0s in the input so far, while $S_{2}$ signifies an odd number. A 1 in the input does not change the state of the automaton. When the input ends, the state will show whether the input contained an even number of 0s or not. If the input did contain an even number of 0s, $M$ will finish in state $S_{1}$, an accepting state, so the input string will be accepted.

The language recognized by $M$ is the regular language given by the regular expression ((1*) 0 (1*) 0 (1*))*, where * is the Kleene star, e.g., 1* denotes any number (possibly zero) of consecutive ones.

Closure properties

If DFAs recognize the languages that are obtained by applying an operation on the DFA recognizable languages then DFAs are said to be closed under the operation. The DFAs are closed under the following operations.

• Union
• Intersection
• Concatenation
• Negation
• Kleene closure
• Reversal
• Init
• Quotient
• Substitution
• Homomorphism

For each operation, an optimal construction with respect to the number of states has been determined in the state complexity research. Since DFAs are equivalent to nondeterministic finite automata (NFA), these closures may also be proved using closure properties of NFA.

As a transition monoid

A run of a given DFA can be seen as a sequence of compositions of a very general formulation of the transition function with itself. Here we construct that function.

For a given input symbol $a\in \Sigma$, one may construct a transition function $\delta _{a}:Q\rightarrow Q$ by defining $\delta _{a}(q)=\delta (q,a)$ for all $q\in Q$. (This trick is called currying.) From this perspective, $\delta _{a}$ "acts" on a state in Q to yield another state. One may then consider the result of function composition repeatedly applied to the various functions $\delta _{a}$, $\delta _{b}$, and so on. Given a pair of letters $a,b\in \Sigma$, one may define a new function ${\widehat {\delta }}_{ab}=\delta _{a}\circ \delta _{b}$, where $\circ$ denotes function composition.

Clearly, this process may be recursively continued, giving the following recursive definition of ${\widehat {\delta }}:Q\times \Sigma ^{\star }\rightarrow Q$:

${\widehat {\delta }}(q,\epsilon )=q$, where $\epsilon$ is the empty string and

${\widehat {\delta }}(q,wa)=\delta _{a}({\widehat {\delta }}(q,w))$, where $w\in \Sigma ^{*},a\in \Sigma$ and $q\in Q$.

${\widehat {\delta }}$ is defined for all words $w\in \Sigma ^{*}$. A run of the DFA is a sequence of compositions of ${\widehat {\delta }}$ with itself.

Repeated function composition forms a monoid. For the transition functions, this monoid is known as the transition monoid, or sometimes the transformation semigroup. The construction can also be reversed: given a ${\widehat {\delta }}$, one can reconstruct a $\delta$, and so the two descriptions are equivalent.

Local automata

A local automaton is a DFA for which all edges with the same label lead to a single vertex. Local automata accept the class of local languages, those for which membership of a word in the language is determined by a "sliding window" of length two on the word.

A Myhill graph over an alphabet A is a directed graph with vertex set A and subsets of vertices labelled "start" and "finish". The language accepted by a Myhill graph is the set of directed paths from a start vertex to a finish vertex: the graph thus acts as an automaton. The class of languages accepted by Myhill graphs is the class of local languages.

Random

When the start state and accept states are ignored, a DFA of $n$ states and an alphabet of size $k$ can be seen as a digraph of $n$ vertices in which all vertices have $k$ out-arcs labeled $1,\ldots ,k$ (a $k$-out digraph). It is known that when $k\geq 2$ is a fixed integer, with high probability, the largest strongly connected component (SCC) in such a $k$-out digraph chosen uniformly at random is of linear size and it can be reached by all vertices. It has also been proven that if $k$ is allowed to increase as $n$ increases, then the whole digraph has a phase transition for strong connectivity similar to Erdős–Rényi model for connectivity.

In a random DFA, the maximum number of vertices reachable from one vertex is very close to the number of vertices in the largest SCC with high probability. This is also true for the largest induced sub-digraph of minimum in-degree one, which can be seen as a directed version of $1$-core.

Advantages and disadvantages

DFAs are one of the most practical models of computation, since there is a trivial linear time, constant-space, online algorithm to simulate a DFA on a stream of input. Also, there are efficient algorithms to find a DFA recognizing:

• the complement of the language recognized by a given DFA.
• the union/intersection of the languages recognized by two given DFAs.

Because DFAs can be reduced to a canonical form (minimal DFAs), there are also efficient algorithms to determine:

• whether a DFA accepts any strings (Emptiness Problem)
• whether a DFA accepts all strings (Universality Problem)
• whether two DFAs recognize the same language (Equality Problem)
• whether the language recognized by a DFA is included in the language recognized by a second DFA (Inclusion Problem)
• the DFA with a minimum number of states for a particular regular language (Minimization Problem)

DFAs are equivalent in computing power to nondeterministic finite automata (NFAs). This is because, firstly any DFA is also an NFA, so an NFA can do what a DFA can do. Also, given an NFA, using the powerset construction one can build a DFA that recognizes the same language as the NFA, although the DFA could have exponentially larger number of states than the NFA. However, even though NFAs are computationally equivalent to DFAs, the above mentioned problems are not necessarily solved efficiently also for NFAs. The non-universality problem for NFAs is PSPACE complete since there are small NFAs with shortest rejecting word in exponential size. A DFA is universal if and only if all states are final states, but this does not hold for NFAs. The Equality, Inclusion and Minimization Problems are also PSPACE complete since they require forming the complement of an NFA which results in an exponential blow up of size.

On the other hand, finite state automata are of strictly limited power in the languages they can recognize; many simple languages, including any problem that requires more than constant space to solve, cannot be recognized by a DFA. The classic example of a simply described language that no DFA can recognize is bracket or Dyck language, i.e., the language that consists of properly paired brackets such as word "(()())". Intuitively, no DFA can recognize the Dyck language because DFAs are not capable of counting: a DFA-like automaton needs to have a state to represent any possible number of "currently open" parentheses, meaning it would need an unbounded number of states. Another simpler example is the language consisting of strings of the form aⁿbⁿ for some finite but arbitrary number of a's, followed by an equal number of b's.

See also

• Acyclic deterministic finite automata
• DFA minimization
• Monadic second-order logic
• NFA to DFA conversion
• Quantum finite automata
• Read-only right moving Turing machines
• Separating words problem
• Turing machine
• Two-way deterministic finite automaton

References

• Hopcroft, John E.; Motwani, Rajeev; Ullman, Jeffrey D. (2001). Introduction to Automata Theory, Languages, and Computation (2 ed.). Addison Wesley. ISBN 0-201-44124-1. Retrieved 19 November 2012.
• Lawson, Mark V. (2004). Finite automata. Chapman and Hall/CRC. ISBN 1-58488-255-7. Zbl 1086.68074.
• McCulloch, W. S.; Pitts, W. (1943). "A Logical Calculus of the Ideas Immanent in Nervous Activity". Bulletin of Mathematical Biophysics. 5 (4): 115–133.
• Rabin, M. O.; Scott, D. (1959). "Finite automata and their decision problems". IBM J. Res. Dev.: 114–125.
• Sakarovitch, Jacques (2009). Elements of automata theory. Translated from the French by Reuben Thomas. Cambridge: Cambridge University Press. ISBN 978-0-521-84425-3. Zbl 1188.68177.
• Sipser, Michael (1997). Introduction to the Theory of Computation. Boston: PWS. ISBN 0-534-94728-X.. Section 1.1: Finite Automata, pp. 31–47. Subsection "Decidable Problems Concerning Regular Languages" of section 4.1: Decidable Languages, pp. 152–155.4.4 DFA can accept only regular language